17 misconceptions about SNARKs (and why they hold us back)

SNARKs are an important cryptographic tool that open up exciting new possibilities in system design – especially in decentralized settings, where they can help mutually distrusting parties cooperate and transact. In this piece, I’m going to talk about some of the misconceptions that I’ve seen as the technology has made rapid advances in the past few years. But first, a quick reminder of what SNARKs are and their importance in crypto and beyond. 

SNARKs allow data to be processed by potentially adversarial entities, who can then prove that the data is valid and has been processed correctly, without having to publish the actual data. For example, a layer-two rollup can prove to an untrusting “verifier” (such as the Ethereum blockchain) that they know some data satisfying certain properties, such as a batch of valid transactions whose execution leads to a given global state. In this way, the Ethereum blockchain itself doesn’t have to do the work of processing the transactions, or even store the data (although rollups often do post enough data to the blockchain to ensure that the state is reconstructable). 

If a SNARK satisfies a property called zero-knowledge, then it can also be useful for privacy preservation; for example, letting someone prove that they deposited money into a mixing pool (and are therefore entitled to withdraw funds from the pool), without revealing which deposit transaction was theirs. Entities can also selectively disclose additional information for compliance purposes, such as their presence on a whitelist or absence from a blacklist, or that they transferred appropriate tax payments to a designated address without revealing additional sensitive information (e.g., specifics of the tax calculation). SNARKs also have many potential applications outside of blockchains, facilitating trust when it otherwise may not exist. 

Originating in the 1980s and ’90s, SNARKs have only recently moved from theory to practice, propelled by advances made by researchers, engineers, and developers in web3. I’ve previously discussed how SNARKs are designed, as well as their performance and security, and the history of their development. 

But as advances in SNARKs accelerate, and the community of people who see the beauty and power of this technology grows, it’s important to be precise in how we think and talk about them. The design space is complex and subtle, leading to a variety of misconceptions and errors that slow down progress and cause untold frustration. I’ve compiled a list of these misconceptions and try to clear them up here. I hope this list will be useful to the community and to anyone building on top of SNARKs, and I welcome suggestions for others you’d like me to address in a future post.

People regularly use the term “ZK proof” to refer to succinct arguments that are not in fact zero-knowledge. Similarly, ZK-rollups typically do not use zero-knowledge proofs, merely succinct ones. 

“Succinct” means that the proofs are short and fast to verify. But “zero-knowledge” means that the proofs leak no information about the “witness” that the prover is claiming to know. Succinctness is about (verifier) performance, while zero-knowledge is about privacy of the prover’s sensitive data.   

The practice of using “ZK-proof” to refer to all succinct arguments may have begun because the first large-scale deployment of SNARKs, ZCash, was actually zero-knowledge, so the terminology was accurate in reference to that particular project. It is also possible that people simply did not have a short-hand for the term “succinct argument,” and started using ZK despite its inaccuracy (“SNARK-based rollup” is not as fun and easy to say as “ZK-rollup”). 

As a community, we should be more precise. While technical specialists may be able to parse the intended meaning, I regularly talk to people who are totally confused by this – especially because “ZK” does have a precise technical meaning. 

This isn’t just pedantic. There are real risks in expecting everyone to somehow differentiate settings in which the term is being used precisely from those in which it is not. Someone may conclude that a SNARK library satisfies zero-knowledge because it refers to itself as “ZK” – even though it leaks information about the witness – leading them to dangerously deploy a non-zero-knowledge library in a privacy-critical application. 

My recommendations: I find the terms “verifiable rollup” or “validity rollup” in place of “ZK-rollup” to be intuitive. When I want to refer to a succinct argument (which may or may not be zero-knowledge), I say SNARK or “succinct argument” rather than ZK-proof. In contexts in which it is important to highlight that the SNARK is zero-knowledge, I say “zkSNARK”.

The S in SNARK stands for “succinct,” which broadly refers to proof systems with short proofs and fast verifiers. While this seems straightforward enough, people mean different things quantitatively when they use the word “succinct,” leading to confusion.

Many authors use the term “succinct” to refer to protocols with proof length and verifier time that is at most polylogarithmic in the runtime of the witness-checking procedure.  Others go even further and use it to refer only to constant-sized proofs. I, however, use it to mean sublinear rather than polylogarithmic or constant. 

I’d argue that others should adopt this practice: First, the “right” definition of succinct should capture any protocol with qualitatively interesting verification costs – and by “interesting,” I mean anything with proof size and verifier time that is smaller than the associated costs of the trivial proof system. By “trivial proof system,” I mean the one in which the prover sends the whole witness to the verifier, who checks it directly for correctness. Moreover, once one designs a proof systems with interesting verification costs ([latex]\sqrt{nλ}[/latex] hashes, for example), one can, through SNARK composition, further reduce costs without a significant increase in prover time. 

Second, superior asymptotics don’t always translate to superior concrete performance. (See for example the comparison of the Ligero and FRI polynomial commitments in #16, below.) 

If we insist that a proof system has polylogarithmic verification costs to qualify as a SNARK, then we have to use totally different terminology to refer to a project using Ligero’s polynomial commitment (whose verifier performs about [latex]\sqrt{nλ}[/latex] hashes) rather than FRI (whose verifier performs about λ  log(n)² hashes). This would be bad: The resulting protocols have the same security properties, and the proof-size advantages of FRI don’t even kick in until the statements being proven are larger than those actually arising in some applications (while prover advantages of Ligero are present at all sizes).

To be even more precise and inclusive, I use “succinct” to refer to any protocol with sublinear proof size, and “work-saving” to refer to any protocol with sublinear verification time. This ensures that SNARKs with small proofs but linear-time verification (like those based on the IPA/Bulletproofs polynomial commitment scheme) do indeed qualify as SNARKs. 

Why do many authors use polylogarithmic verification costs as their standard for ”succinct”? This practice stems from the fact that, in theoretical contexts, polylogarithmic cost is viewed as a natural place to draw a line, mirroring the way ”Polynomial Time” is deemed the benchmark for an “efficient” algorithm in theoretical computer science (even though many polynomial-time algorithms are hopelessly impractical). 

But SNARK design has less in common with the study of polynomial-time algorithms than it does with the field of sublinear algorithms, which studies how to process inputs that are so big that algorithms cannot afford to read or store the whole thing. Like the study of SNARKs today, sublinear algorithms are heavily motivated by practical considerations. And just as there is always a trivial proof system in which the prover sends the whole witness to the verifier, in sublinear algorithms there is always a trivial solution of linear cost (namely, read and store the whole input). 

So just as the field of sublinear algorithms chose to be inclusive – declaring any solution with sublinear costs to be an interesting one – we should do the same for SNARKs. 

I am asked to explain the distinction between SNARKs and STARKs so frequently that I have to discuss their meanings here.

SNARK stands for Succinct Non-interactive ARgument of Knowledge. I’ve already addressed the meaning of “succinct.” “Non-interactive” means the verifier does not have to send any challenges to the prover, so the proofs can (for example) be posted on the blockchain for any blockchain node to verify at its leisure. “ARgument of Knowledge” means that the only way a polynomial-time prover can find a convincing proof that it knows a witness is to actually know the witness.

STARK was introduced in the scientific literature as having a precise technical meaning. It stands for Scalable Transparent ARgument of Knowledge. (Many people quite reasonably think the S means “succinct” as it does in SNARK; see section 3.3 of this paper.) But here, “scalable” means that the prover time is at most quasilinear (i.e., linear up to logarithmic factors) in the runtime of the witness-checking procedure, and that verification costs (time and proof size) are at most polylogarithmic in this runtime. “Transparent” means that the proof system does not require a trusted setup. Under this technical definition, many STARKs exist today. 

So what are the sources of confusion, and their consequences? There are at least three.

**First, in public discourse, the meaning of “STARK,” like the term “ZK,” has deviated substantially from the technical meaning I explained above. The term is now typically used to refer specifically to the proof system of StarkWare (which incorporates Stark into their brand name) and its close derivatives. 

An important clarification here is that the term “STARK” does not specify whether or not the protocol is interactive. As far as I am aware, STARKs today are exclusively deployed non-interactively (which makes them SNARKs). This has led to substantial confusion in public discussion regarding the security of deployed proof systems. 

**Second, when a proof system is deployed interactively, much lower security levels may be appropriate than when the proof system is deployed non-interactively. An adversary attacking an interactive deployment cannot know if an attempted attack will succeed without interacting with the verifier, which drastically slows the speed and increases the cost of attempting an attack, and makes the attack apparent to the verifier. Furthermore, stronger cryptographic assumptions underlie non-interactive deployments relative to interactive ones. 

Because the term “STARK” does not specify whether or not the protocol is interactive, it confuses any discussion about acceptable security parameters for deployments. After I published my previous blog post on this topic, multiple people reached out to tell me that they believed that current deployments of STARKs are interactive, and hence low security levels are appropriate. They were mistaken.  

**Third, the introduction of the term “STARK” has caused many in the community to abuse the term “SNARK,” misusing it to refer specifically to SNARKs with a trusted setup, such as Groth16 and its predecessors. This is done to distinguish those SNARKs from StarkWare’s and its descendants. 

Recommendation: We don’t need a different acronym for every collection of properties that a protocol might satisfy, especially if it leads to confusion regarding central issues like appropriate security levels. The term “transparent SNARK” is perfectly clear and should be used to refer to any transparent SNARK. If an interactive analog is ever deployed, it can simply be called a transparent interactive argument. (In this post, I do use the term “STARK” to refer to the proof system of StarkWare and its derivatives, because some of the misconceptions described here apply specifically to those proof systems.)

Many projects today are using classes of constraint systems that are overly tailored to specific back-ends. As a consequence, people often fail to distinguish between the constraint systems themselves and the back-ends to which they are tailored. Moreover, the community has until now failed to recognize that back-ends different from the ones to which these constraint systems are tailored can nonetheless prove statements about them (and with performance benefits to boot). 

These misconceptions have led to incorrect assertions, in both the scientific literature and in public discourse, about the relative performance of different backends. As a result, projects are misdirecting effort and deploying SNARKs with suboptimal performance. 

Context.

• SNARKs are typically deployed by first applying a front-end, which turns the appropriate witness-checking procedure into a kind of circuit; and then applying a back-end, that is, a SNARK for circuit-satisfiability. 
• “Plonkish” refers to a kind of circuit (or, more precisely, a constraint system) that the Plonk back-end can prove statements about. 
• Algebraic Intermediate Representation (AIR) refers to another kind of circuit (roughly, a particularly structured kind of Plonkish circuit) that the STARK back-end can prove statements about. 

A common misconception is that Plonk is the only back-end that can prove statements about Plonkish circuits, and STARKs are the only back-end that can prove statements about AIR. In fact, people often fail to distinguish between “Plonkish” (which is a kind of constraint system), and Plonk (a particular back-end that can prove statements about Plonkish constraint systems). I have also encountered a similar failure to distinguish between AIR and the STARK back-end. 

The confusion is understandable. Indeed, on top of confusing naming conventions, definitions of Plonkish and AIR are often tailored to low-level details of how the Plonk and STARK back-ends work. 

What’s really going on. Most SNARKs can be easily tweaked to support both Plonkish and AIR. 

The main exception is Groth16 and its predecessors, which are limited to “degree-2 constraints” and achieve their fastest verification in particular for a subclass of degree-2 constraint systems called “rank-one constraints” (R1CS). (Incidentally, many people don’t realize that Groth16 and its predecessors can be modified to support arbitrary degree-2 constraints, not only rank-one. The verifier’s costs grow with the rank of the constraints, but can be brought back down via recursion. See #6, below.)

Some seem to have an essentially backwards conception of the relative generality of various SNARKs. Plonk and its descendants such as Hyperplonk cannot handle R1CS without overheads for the prover. But SNARKs such as Spartan and Marlin – which were originally described as targeting R1CS, and often written off for not supporting popular classes of circuits like Plonkish and AIR – can handle this. 

In fact, Spartan and Marlin support a clean generalization of R1CS, Plonkish, and AIR called Customizable Constraint Systems (CCS) (see Figure 1 below). And they do so with performance benefits. For example, Plonk requires the prover to commit to the value of every “wire” in a circuit, and uses so-called copy constraints to ensure that the values assigned to every wire coming out of a single gate are equal. These commitment costs are typically the prover bottleneck. Accordingly, engineers using Plonk and its variants have devoted significant effort to developing notions such as “relative references,” with the goal of minimizing copy constraints in Plonkish circuits.

In Spartan, when dealing with circuits with repeated structure, the prover only commits to one value per multiplication gate in the circuit. There are always fewer gates than wires (typically by a factor of at least 2). And addition gates “come for free” when Spartan is applied to circuits with repeated structure: Addition gates do not add to the prover’s commitment costs and do not contribute to the prover’s other costs besides increasing the work required for “direct witness-checking,” that is, the work required to evaluate the circuit on the witness with no guarantee of correctness.

Despite their popularity, the notions of AIR and Plonkish circuits are overly motivated by low-level details of the Plonk and STARK back-ends. There are conceptual and performance benefits to modularity, which in this context means clearly separating the kind of circuit used to represent the witness-checking procedure from the back-end used to prove satisfiability of that circuit. 

Recommendation. I advocate for using a constraint system like CCS, which is defined in the same spirit as R1CS, involving only matrix-vector products and Hadamard (i.e., entry-wise) vector products. Just as R1CS is clearly distinct from popular back-ends like Groth16 that are used to prove it, CCS is clearly separated from any particular back-end used to prove statements about it. And CCS captures, without overheads, all of the most popular constraint systems used in practice today.

Context. A lookup argument is a specialized SNARK that can be combined with general-purpose SNARKs to greatly reduce the size of circuits the general-purpose one ingests. The notion of lookup arguments in SNARK design was introduced in Arya, which described them in the context of arithmetic circuits of fan-in two, a special case of R1CS. 

Given this, I do not know how the misconception came about that SNARKs for R1CS cannot interface with lookup arguments. Perhaps it has something to do with Plookup, a popular lookup argument originally presented using techniques inspired by the Plonk back-end. But similarly to how Plonk is not the only back-end that supports “Plonkish circuits,” Plonk is not the only back-end that can prove satisfiability of the constraint system implicit in Plookup. 

Many lookup arguments boil down to a “grand product” argument – computing the product of a large number of committed values. Grand products can be computed efficiently by arithmetic circuits of fan-in 2 (via a binary tree of multiplication gates), which are a very special case of R1CS. One may not want to use a SNARK for R1CS as a black box when computing a grand product, but rather modify the techniques underlying the SNARK for R1CS to exploit the special structure of grand products for improved concrete efficiency (for example, see sections 5 and 6 of this paper). 

Ramifications. This misconception leads to substantial errors in published estimates of the relative performance of different SNARKs. A typical mistake is to run SNARKs that were originally described as targeting R1CS on circuits that are more than an order of magnitude larger than those fed to SNARKs described as targeting Plonkish, with the justification that the former cannot support lookups or high-degree constraints. The experimenter then naturally concludes that the latter SNARK is faster than the former. But they reach this conclusion simply because the former was run on a much larger circuit than necessary. 

A related (but more general) error is to combine a back-end with a polynomial commitment scheme with large evaluation proofs, and then conclude that the back-end inherently has large proofs. In fact, the proof size is mainly determined by the choice of polynomial commitment scheme. And for the most part, any SNARK can use any polynomial commitment scheme, the main complication being that some SNARKs require commitments to multilinear polynomials and others to univariate ones.

Recommendations. Understanding which front-end techniques (and other optimizations) can be combined with which back-ends can be challenging. As a result, SNARK designers arrive at inaccurate conclusions about the relative performance of different back-ends.

Some confusion is unavoidable because new front-end techniques (and other optimizations) are often described in the context of specific back-ends, even though they apply more generally. Also, existing back-ends may need to be modified to interface with new front-ends and other optimizations. 

But we can and should improve this state of affairs. For instance, the community can encourage a deeper understanding of the back-ends originally described as targeting R1CS, which until now have been maligned as incapable of interfacing with certain front-end techniques. And we can encourage people to make more serious efforts to modify existing back-ends before asserting that they cannot interface with new front-ends or other optimizations. Finally, to the extent possible, different back-ends should be compared using the same polynomial commitment scheme.

Context. Groth16 requires a circuit-specific trusted setup; proving satisfiability of a new circuit requires running a new trusted setup. Plonk has a universal setup, meaning that a single setup supports all circuits up to a specified size bound. One might expect that the Plonk prover should pay a performance price for achieving a universal setup, yet many people believe that the Plonk prover is actually faster than the Groth16 prover. 

The truth is more nuanced.

Details. Plonk cannot support R1CS without overheads. Groth16 targets R1CS but cannot support Plonkish circuits. As a result, the types of circuits they support are incomparable. But both do support circuits with addition and multiplication gates of fan-in two, and when applied to such circuits Groth16 is actually faster than Plonk. 

Specifically, Plonk requires the prover to do 11 multi-scalar-multiplications (MSMs), each of length equal to the number of gates in the circuit, meaning both multiplication and addition gates.

Groth16 needs just 3 MSMs on group G₁ and 1 MSM on G₂ (where G₁  and G₂ are groups equipped with a pairing). Moreover, for Groth16 each of these MSMs is of size equal only to the number of multiplication gates only (addition gates are “free” in Groth16). MSMs over G₂ are roughly 2-to-3 times slower than over G₁, so this equates to 5 to 6 MSMs over G₁, each of size equal to the number of multiplication gates. This could be many times faster than the Plonk prover’s work, depending on the number of addition gates.

Many people believe that Plonk is faster than Groth16 because, for some important applications, Plonkish circuits can be substantially smaller than R1CS instances capturing the same application (examples include MinRoot and Pedersen hashing). But taking advantage of this requires having the time and expertise to write an optimized Plonkish circuit (unless, of course, someone else has already done that work). This work is often done by hand, although it’s conceivable that future compilers may be able to automatically leverage the full expressive power of Plonkish circuits. The way it’s done today is time-intensive and difficult (and any error in specifying the Plonkish constraint system will destroy the security of the system). 

Moreover, as mentioned in #5 above, many people don’t realize that Groth16 and its predecessors can be modified to support arbitrary degree-2 constraints, not only rank-one. (Non-rank-one constraints are sometimes called custom constraints.) The limitation of Groth16 is in being unable to move beyond degree-2 constraints, not in lack of support for custom constraints. (Another little-known fact is that predecessors of Groth16 such as Zaatar can handle high-degree constraints, but they yield two-round, private-coin arguments, so they do not allow on-chain verification.) 

The bottom line. Plonk can yield a faster prover than Groth16 – but not always. And even when it can, making this happen often requires considerable expertise and time investment on the part of the developer.

The only cryptographic primitive used in STARKs is cryptographic hash functions. SNARKs based on elliptic-curve cryptography (ECC) assume that the discrete logarithm problem is hard to solve in certain elliptic curve groups (and may make other assumptions as well). 

I would agree with the spirit of this statement if FRI were being deployed under parameters proven to achieve the targeted security level in the random oracle model, but this is not the case. FRI-based SNARKs today are pervasively deployed under unproven conjectures that known attacks on FRI are exactly optimal. This is done to control the proof size and verification costs. (See my previous post for details of the conjectures, and #9 below for their performance implications.) 

Here, FRI is the popular polynomial commitment scheme underlying STARKs, whose proofs consist of O(λ  log(n)[latex]^2[/latex]) many hash evaluations when applied to polynomials of degree n at λ bits of security. To be more precise, FRI is a means to test whether a committed function is low degree (see this lecture for my best attempt at an exposition), and it can be used to give a polynomial commitment scheme (see slides 59-65 of the aforementioned lecture). 

In summary, while it is possible to deploy STARKs under conservative security assumptions, existing projects do not do so.

For polynomial commitment schemes, choices of parameters can significantly impact prover runtime and proof size. This holds in particular for those that only use hashing (e.g., FRI, Ligero, Brakedown, etc.) 

In deployed SNARKs from this class, there are major differences in both the field size and the so-called blowup factor B, which controls a tradeoff between prover time and proof size. Prover time is linear in B while proof size is linear in 1/log(B). For example, a blowup factor of 16 can lead to 4x smaller proofs than a blowup factor of 2, but causes the prover to be 8x slower.

Some projects compose a FRI-based SNARK with an elliptic-curve-based one, to shrink the FRI proof size before posting on-chain. These projects can configure the FRI prover to be faster, with bigger proofs, since the FRI proofs are not directly posted on-chain. Others do post FRI proofs directly on-chain, and hence configure the prover to be substantially slower. 

Concretely, if running FRI with a blowup factor of 16 over a 251-bit field, the prover may be over 10x times slower for a given polynomial degree bound, compared to using a blowup factor of 4 and (an extension of) a 64-bit field. In this comparison, a factor of 4 comes directly from the 4x bigger blowup factor, and the remainder comes from the larger field (as the larger field makes FFTs and Merkle-hashing more than 4x slower).

This is a standard characterization of proof lengths for FRI and STARKs. But FRI proofs are in fact multiple hundreds of KBs at 100+ bits of security, even under the conjectures discussed in #7, above, that known attacks are exactly optimal. 

For example, with a FRI blowup factor of 4, applying the most straightforward implementation of FRI to a polynomial of degree 2²⁰  at 128 bits of security (even under aggressive soundness conjectures) leads to proofs nearly 500 KiBs in size. This can be brought down by certain optimizations such as “grinding,” “Merkle-capping,” and “early stopping” (discussed in #16, below). However, these techniques will not reduce proof sizes below 200 KiBs. 

The “dozens of KBs” characterization appears to refer to the configuration of FRI discussed in my previous blog post. This configuration targets 80 bits of security, under aggressive conjectures, with 32 of the bits coming from the grinding technique, and only 48 coming from FRI itself. Moreover, this configuration uses a large blowup factor of 16, leading to a slow prover. The SHARP verifier discussed in that blog post has subsequently been changed to a higher-security configuration, but the StarkEx dYdX verifier today remains in the configuration discussed in the post. 

Increasing 80 bits to 128 bits doubles the proof size. Reducing the blowup factor from 16 to 4 to obtain a more reasonable prover time doubles proof size again. Removing the aggressive security conjectures, discussed in #7, above, doubles (at least) proof size again. Lowering the bits of security contributed by grinding from 32 to, say, 16 (as using grinding to obtain 32 bits of security forces the honest prover to perform 2³² hashes) increases the proof size another 33 percent. 

These increases are the difference between dozens of KBs and hundreds.

Context. In a multiplicative group, a group operation takes as input two group elements g₁, g₂, and outputs their (group) product g₁ * g₂. A group exponentiation refers to taking some group element g and raising it to some power x. That is, an exponentiation computes the value g^x given as input g and the exponent x. 

In general, the exponent x may be any number between 1 and the size |G| of the group. The total number of group operations (i.e., multiplications) required to compute the exponentiation via the standard square-and-multiply algorithm is about 3/2 log |G|. Cryptographic groups have size at least about 2²⁵⁶.  So a group exponentiation can be roughly 400 times slower than a group operation.

Yet many papers on SNARKs refer to group exponentiations as group operations. We as a community cannot have a clear understanding of SNARK performance if we don’t distinguish between factors of 400x in prover runtime.

Recommendation. I am not sure whether the underlying issue here is careless accounting or a lack of awareness that these operations have substantially different costs (both asymptotically and concretely). However, I suspect it’s the latter: it’s hard to imagine that protocol designers would intentionally gloss over such a large difference in costs. 

We as a community must increase awareness of the actual costs of these operations, and encourage more precise cost accounting in papers and presentations. A stronger emphasis on implementation, and more careful benchmarking, would also be helpful. 

Context. A multi-exponentiation of size n computes an expression of the form 

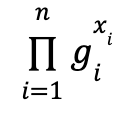
That is, the multi-exponentiation operation outputs the product of the results of n exponentiations. This is also often called an MSM (multi-scalar multiplication) based on additive group notation.

Naively computing a multi-exponentiation entails performing each of the n exponentiations independently (each at the cost of 3/2 log |G| group operations) and multiplying the results together. However, a famous algorithm of Pippenger computes multi-exponentiations with roughly a factor log n fewer group operations than this naive algorithm (see section 4 in this paper for a nice exposition). This “Pippenger speedup” can easily be a factor of 20 or more in practice if n is several million or larger. 

Many papers that fail to distinguish between group operations and exponentiations also fail to distinguish between n exponentiations and multi-exponentiations of size n, leading to additional imprecision about concrete performance costs. 

Recommendation. As with #10, the remedy is a combination of improved awareness of the actual costs of these operations, more precise cost accounting, and a stronger focus on implementation and benchmarking.

A SNARK has λ bits of security if an attacker must perform about 2^λ work to find a convincing proof of a false statement with probability close to 1. 

Asymptotically, the security parameter must be super-logarithmic in the input size to guarantee security against superpolynomial time adversaries. That is, λ should be treated as larger than any logarithmic factor.

Concretely, λ should be 128 and up. This is 3-to-6 times larger than log(n) for practical input sizes n. It’s acceptable to think of λ as about 4*log(n) in practice – but don’t forget the factor of 4. 

Replacing a log(n) factor in a SNARK with a λ factor makes the SNARK more expensive rather than less, both concretely and asymptotically.

The misconception. The example below involving sequential repetition reveals that applying Fiat-Shamir to an r-round interactive protocol can lead to a factor-r loss in the number of bits of security. Many in the community believe that sequential repetition is the primary natural technique that yields interactive protocols for which such a loss occurs. In fact, there are others.

Context and example. Taking a one-round interactive protocol with soundness error ½ (i.e., “1 bit of interactive security”) and repeating it λ times sequentially obtains a λ-round interactive protocol with soundness error 2^-λ (i.e, “λ bits of interactive security”). Applying the Fiat-Shamir transformation to this λ-round protocol may lead to a totally insecure result: a so-called grinding attack can find a convincing proof of any false statement with only about λ hash evaluations (i.e., the Fiat-Shamir-ed protocol has only log(λ)-bits of security). 

In this attack on the Fiat-Shamir-ed protocol, the cheating prover attacks each round individually. First, it grinds over prover messages in the first repetition until it finds one that hashes to a “lucky” verifier response. In expectation, this only requires trying out 2 prover messages (because soundness error ½ means that any particular prover message yields a lucky verifier response with probability ½, so after trying two messages, the prover expects to have found a lucky one). 

Once it finds such a prover message m₁, it is done attacking the first repetition. It fixes the round-one message to m₁, and moves on to grinding over prover messages for the second repetition, until it finds one that hashes to a lucky verifier response. Again, in expectation this requires only 2 hashes – and so on, until all repetitions have been successfully attacked.

The reality. Parallel repetition combined with Fiat-Shamir can also lead to a major loss of security. (The attack was first presented by Attema, Fehr, and Klooß.) 

Suppose, for example, you take a 2-round base protocol (i.e., the verifier sends two messages to the prover) with 64 bits of interactive security and repeat it twice in parallel, obtaining a two-round protocol with 128-bits of interactive security. For a prover to convince the verifier to accept in both repetitions, it will have to get lucky in both repetitions, which happens with probability 2^-64*2^-64=2^-128. If you then apply Fiat-Shamir to render the protocol non-interactive, it will have at most 64 bits of security, essentially the same as if you hadn’t repeated the base protocol at all. 

The attack on the Fiat-Shamir-ed protocol once again attacks one repetition at a time. The attacker grinds over first messages m1 until it gets a lucky verifier challenge in just one out of the two repetitions. (By “lucky,” we mean that the attacker can easily pass all of the verifier’s checks in that particular repetition of the base protocol.) In expectation, at most 2⁶⁴ hash evaluations are needed before the attacker finds such a message m₁. Fixing m₁, it then grinds over messages m₂ until it gets a lucky verifier challenge in round 2 of the other repetition of the base protocol. Again, only about 2⁶⁴ hash evaluations will be needed before a lucky message is found. At that point, both repetitions of the base protocol have been compromised by the attacker. 

Recommendation. The upshot is that if one wishes to apply the Fiat-Shamir transformation to an interactive protocol with multiple rounds, then, to rule out a major security loss, one really should show that the interactive protocol satisfies a strengthened version of soundness, called round-by-round soundness. Round-by-round sound interactive protocols – even if they have many rounds – do not suffer a loss of security when the Fiat-Shamir transformation is applied in the random oracle model. One such example is the sum-check protocol (see section 2.1 of this paper). IPA/Bulletproofs is another many-round protocol known to be secure in the random oracle model when Fiat-Shamir’d. 

Surprisingly, FRI is a logarithmic-round protocol that until now has not been shown to be round-by-round sound – even though all of its deployments that I’m aware of apply Fiat-Shamir to render it non-interactive, and even though multiple research papers have stated security guarantees in terms of FRI’s round-by-round soundness. So, contrary to many previous assertions, SNARKs based on FRI have not been known to be secure in the random oracle model. Fortunately, new work addresses this gap in the existing security analyses. This does not resolve the additional conjectures regarding FRI’s soundness upon which these deployments are based (see #7, above). 

Bonus: A related security pitfall to avoid. While we’re discussing dangers of applying the Fiat-Shamir transformation, please remember to hash any inputs to (or parameters of) the statement to be proven that might be under the control of an adversary. 

Failing to do this allows an attacker to generate a SNARK proof that passes all of the verifier’s checks except for one, and then easily find an input that makes even this final check pass. Over the years, this vulnerability has arisen repeatedly in deployments of protocols that use the Fiat-Shamir transformation. The issue is common enough that we have terminology to refer to it: “Weak Fiat-Shamir.” 

With the Weak Fiat-Shamir vulnerability, the attacker can find false statements and convincing proofs thereof but does not have perfect control over the false statements that it finds. That is, the adversary cannot pick a false statement at will and then find a convincing proof π for it. Rather, the adversary first produces π, and then reverse-engineers a false statement for which π is a convincing proof. Nonetheless, the effects of the vulnerability can be devastating, as explored in the works linked to above.

A lot of nice work has been devoted to designing SNARKs that work over small fields — in particular, fields that are smaller than those used by elliptic curve groups, which are typically size 2²⁵⁶ or larger. The motivation here is that a field operation in a small field (say, the field of size 2⁶⁴ – 2³² + 1) can be substantially faster than the same field operation in a large field. Moreover, some hardware, like GPUs, natively operate on 32-bit data types, making operations on very small fields especially fast. 

The public discussion that I have seen on this issue has missed an important nuance: whether or not it makes sense to use a small field (even when they are an option) is highly application dependent. For example, one of the major tasks of rollup servers is to prove knowledge of ECDSA digital signatures. These are statements over large fields. Working over a small field actually increases proving time when proving knowledge of ECDSA signatures. Each large-field operation required for digital signature verification has to be simulated via many operations over the small field that the SNARK works over. 

For pre-zkEVM rollups, proving knowledge of digital signatures was the prover bottleneck. For example, this may be why Starkware works over a 251-bit field that matches certain ECDSA signatures, not a smaller field. (The EVM involves enough complicated logic, such as Merkle-Patricia trie updates, that proving knowledge of signatures may not be the bottleneck for zkEVMs.) 

For another example, the EVM uses 256-bit words as its word size. If one works over a field of size less than 2²⁵⁶, one has to allocate multiple field elements to represent a single uint256 data type. This is especially painful when using field sizes that are just less than a power of 2 (such as the Goldilocks field). For example, a 251-bit field is “just a bit too small” to represent a uint256 data type. This roughly doubles the prover costs required to support these data types. 

My thoughts. Large fields are also a resource that can potentially be exploited to simulate many small-field operations with a single big-field operation. I expect to see more progress on this in the near future. Meanwhile, it’s great to have the option to work over small fields. But it’s not the key to faster SNARKs in all contexts.

Inner product arguments are a generalization of polynomial commitments: they allow an untrusted prover to reveal the inner product of a committed vector with any other vector specified by the verifier. The most well-known inner product argument today is  IPA/Bulletproofs, which has a linear-time verifier. Many projects prioritize sublinear verification, and therefore ignore inner product arguments. Prominent exceptions include the ZCash Orchard protocol and Monero, as the verification time of IPA/Bulletproofs is fast enough for these applications. 

While IPA/Bulletproofs has a linear-time verifier, this is not the end of the story. For example, Dory is a transparent and homomorphic inner product argument with logarithmic verifier time and proof size (though the proof size is concretely an order of magnitude larger than IPA/Bulletproofs). Furthermore, IPA/Bulletproofs, as with all homomorphic commitments, has attractive batching properties that render its verifier sublinear time in contexts where amortization is possible. 

There are additional transparent polynomial commitments directly inspired by the line of work on inner product arguments that have extremely promising cost profiles. An example is Hyrax, which has an extremely fast prover but is not popular today because it has large proofs (square root in the size of the committed polynomial). However, the proof size can be reduced via SNARK composition.

The reality. This depends on the degree of the polynomial being committed. For polynomials of degree up to about 2¹⁸, FRI proofs are actually bigger than an alternative called Ligero. This holds without basing the security of Ligero on any unproven conjectures about statistical security, and while basing the security of FRI on those conjectures (see #7 above). 

Degree-2¹⁸ is admittedly lower than what most projects use today. But some projects plan to use polynomials of this degree in the future to control the substantial memory costs of the FRI prover (which are many GBs).  

If one does not base the security of FRI on the conjectures mentioned in #7 above, then Ligero proofs remain smaller than FRI proofs until the degree is larger than about 2²⁰. (A more detailed comparison can be found here.) 

The upshot is that asymptotic comparisons of different proof systems do not necessarily match their concrete costs until the instance sizes are larger than those arising in practice. Projects applying FRI to polynomials smaller than degree 2²⁰  should consider switching to Ligero for improved performance and avoidance of strong security conjectures.

No, they are not. 

***

Justin Thaler is Research Partner at a16z and an Associate Professor in the Department of Computer Science at Georgetown University. His research interests include verifiable computing, complexity theory, and algorithms for massive data sets.

***

The views expressed here are those of the individual AH Capital Management, L.L.C. (“a16z”) personnel quoted and are not necessarily the views of a16z or its affiliates. a16z is an investment adviser registered with the U.S. Securities and Exchange Commission. Registration as an investment adviser does not imply any special skill or training. Certain information contained in here has been obtained from third-party sources, including from portfolio companies of funds managed by a16z. While taken from sources believed to be reliable, a16z has not independently verified such information and makes no representations about the enduring accuracy of the information or its appropriateness for a given situation. In addition, this content may include third-party information; a16z has not reviewed such material and does not endorse any advertising content contained therein.

This content is provided for informational purposes only, and should not be relied upon as legal, business, investment, or tax advice. You should consult your own advisers as to those matters. References to any securities, digital assets, investment strategies or techniques are for illustrative purposes only, and do not constitute an investment recommendation or offer to provide investment advisory services. Furthermore, this content is not directed at nor intended for use by any investors or prospective investors, and may not under any circumstances be relied upon when making a decision to invest in any fund managed by a16z. (An offering to invest in an a16z fund will be made only by the private placement memorandum, subscription agreement, and other relevant documentation of any such fund and should be read in their entirety.) Any investments or portfolio companies mentioned, referred to, or described are not representative of all investments in vehicles managed by a16z, and there can be no assurance that the investments or investment strategies will be profitable or that other investments made in the future will have similar characteristics or results. A list of investments made by funds managed by Andreessen Horowitz (excluding investments for which the issuer has not provided permission for a16z to disclose publicly as well as unannounced investments in publicly traded digital assets) is available at https://a16z.com/investments/.

Additionally, this material is provided for informational purposes solely and should not be relied upon when making any investment decision. Past performance is not indicative of future results. Investing in pooled investment vehicles and/or digital assets includes many risks not fully discussed herein, including but not limited to, significant volatility, liquidity, technological, and regulatory risks. The content speaks only as of the date indicated. Any projections, estimates, forecasts, targets, prospects, and/or opinions expressed in these materials are subject to change without notice and may differ or be contrary to opinions expressed by others. Please see https://a16z.com/disclosures/ for additional important information.