Zero Gas Wasted: Winning the IAmTheOptimizor Challenge

Gas golfing plays an important role in smart contract engineering. Not only is it a fun and challenging task, but it saves valuable blockspace. So, when 0xBeans launched the gas-golfing challenge “I Am The Optimizor” — we joined in.

For the uninitiated, contestants (smart contract engineers and teams) compete to write a contract that solves the classic 3Sum problem. Contracts are scored by the sum of their gas usage and size. Those with the lowest score steal a special NFT from previous winners  — “a trophy that has only ever been held by those that have been blessed by the optimizor gods,” at least according to the OpenSea description.

So far, the NFT has been claimed by 16 such optimizors — including, most recently, the authors of this post. We outlined the process in a couple of Twitter threads (here and here), but now we’d like to take a deeper dive into how our solution works. We’ll also cover some of the other approaches we built on, and a few unconventional optimizations we used.

The challenge itself is a simple optimizer-themed “king of the hill” game, where players must write smart contracts that adhere to the IPlayer interface, with the goal of using the least amount of gas and having the smallest bytecode size.

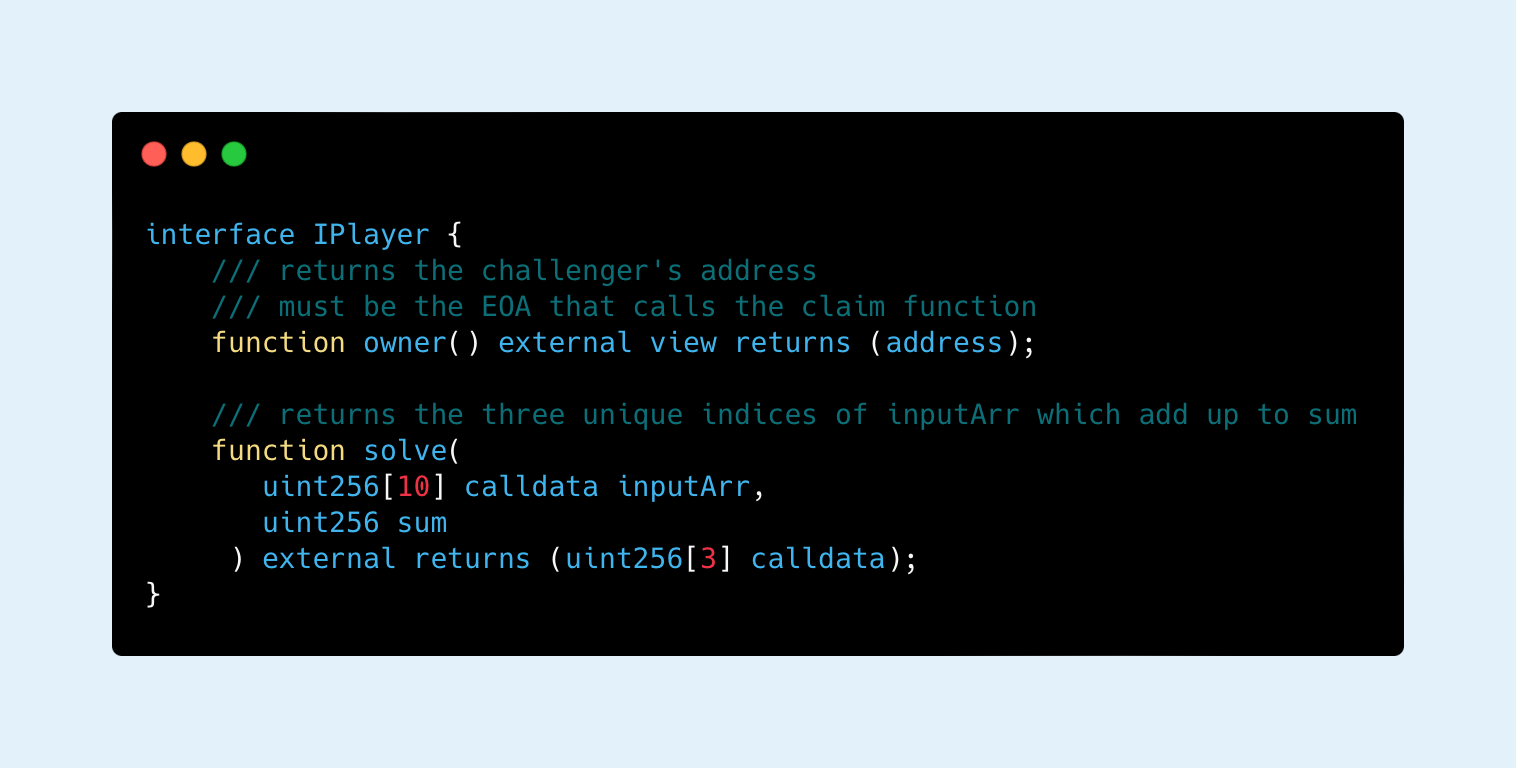
The challenge contract allows contestants to call the claim function, passing in the address of their player contract, and then performs two actions: First, it calls the owner function on the player contract, ensuring that it returns the same address that originally called the claim function (and resulting in a harder challenge with much more interesting solutions). Next, it generates a random inputArr and selects a target sum parameter.

These values are passed to the player contract through the solve function. The player must then correctly calculate the three unique elements in inputArr that add up to sum.

This is the classic 3Sum problem, which many of you may remember from computer science courses and coding interviews; for many students, it is one of the first non-obvious programming problems they encounter.

The contracts are scored based on the sum of their bytecode size and the gas used to call the solve function. The lowest score wins.

Contestants quickly created some impressive contracts.

Naturally, many of these solutions didn’t solve the 3Sum problem at all. Instead, they gamed the contract’s randomness (very efficiently!) by predicting the solution and deploying a contract that returns it. Contestants accomplished this by returning hard-coded values and attempting to submit them as a flashbots bundle every block. By default, flashbots does not allow reverting transactions, so if a player’s contract didn’t happen across an efficient solution, their transaction wouldn’t make it into a block. But if they got lucky, and their solution matched the randomly generated one, then their transaction was included — and they became the optimizer.

The second, less obvious, approach was to make the contract branchless. When calling a smart contract, the function to call is specified by prepending a specific 4-byte sequence called the selector to the beginning of the transaction calldata. The beginning of most contracts start off with a switch statement that alters the execution flow based on this selector.

This process increased the bytecode size and gas usage of submissions (and was thus abandoned by the best contracts) – but it also led to an interesting, though unintuitive, sleight of hand by reading out-of-range calldata: If you readcalldata[0x24..0x44], it will always return zero when the owner function is called; but will return the second element in the array when the solve function is called. This means by using just a singleCALLDATALOAD opcode, you can perform a memory manipulation that behaves differently depending on which function was called.

Contracts that made use of this behavior were able to completely remove the initial selector switch. With this trick and some clever combinations of opcodes, contestants could start writing some very efficient contracts and near-perfect solutions. These led us to an idea for a new optimization to add to the mix — one that built on previous techniques, but layered on a new, unconventional optimization.

The best contract at the time was quite efficient, but was it the most efficient? Here’s what it looked like:

It seemed unlikely that we’d be able to improve on this, but what if we replaced the PUSH2 0x0144 with COINBASE? The cost of a PUSH2 instruction is three gas and three additional bytes to the contract size. This means it contributes six to the total score of the contract. COINBASE, on the other hand, uses two gas and adds just one byte to the contract size for a total score of three. This meant that if we could somehow make COINBASE return 0x0144, we could win by two points.

One small problem: COINBASE usually doesn’t return 0x0144. This makes sense, since the coinbase address is the recipient of the block’s transaction fees (usually the block proposer). The COINBASE opcode returns the block’s coinbase address, which gets set by the Ethereum validator that produces the block. All transaction tips from that block then flow to the coinbase address.

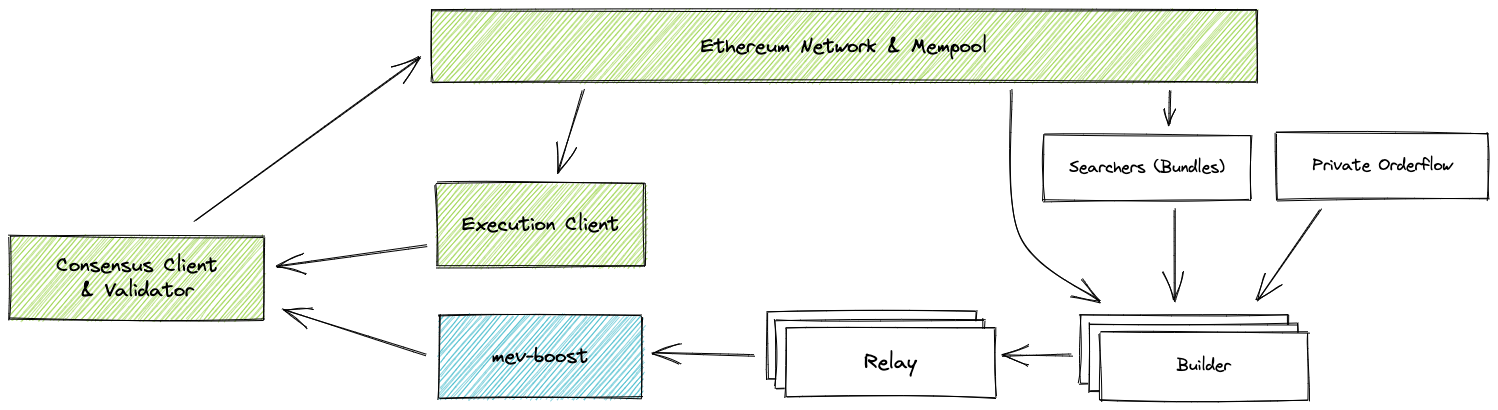
And even if we submitted bundles to flashbots, paying the validator to include the transaction, we would not be able to set the coinbase address. It became clear that we needed to move deeper into the block building infrastructure stack.

But before we dive into the approach we took, let’s look at the current state of proposer-builder separation (PBS):

PBS is the current mechanism in which MEV is extracted on Ethereum (introduced alongside the switch to proof of stake). In PBS, there are independent network participants called “searchers” who submit bundles of transactions that they want to see included in a specific sequence; “builders” who compose bundles and transactions from the mempool into full execution layer Ethereum blocks; and “relays” who take blocks from builders and forward the most profitable one to the validator that is due to propose on that slot. In previous submissions, the players often acted as searchers, submitting their bundles of transactions to builders for inclusion into a block.

To compete in this challenge, we had to move one level deeper into this system — and become block builders ourselves. Block builders compose the entire execution layer block for validators. They run much more complex software than searchers in order to correctly set and compute block parameters. This means they have full control over the block, including the ability to set nearly any field: the state root, logs bloom, receipts root, and, critically, coinbase.

Most block builders set their own address as the coinbase, and pay the validator by sending them a transaction at the very end of the block. However, why couldn’t we just set the coinbase address to 0x0144, and effectively burn the fees in the block? All we had to do was pay the validator with our own funds rather than the proceeds of the block.

Unfortunately, that plan didn’t last long. Top competitors submitted a new contract that beat their previous attempt, and made the process of finding a better contract even more difficult (and interesting).

Was there any way we could still use our coinbase trick? Fortunately, we realized we could combine the coinbase optimization with yet another trick – modifying the gas price.

Here’s the contract we came up with:

To make this contract work, we had to ensure that GASPRICE returned 0x0900000000; COINBASE returned 0x24; and ORIGIN returned an address that began with 0x0n00000000, where n can be any digit between 1 and 8.

We could already set the coinbase with our block builder and easily modulate the gas price using the transaction tip, but we still needed to generate 10-nibble vanity addresses from which to originate transactions. This was easy using the famously insecure Profanity address generator. (We’ll leave it as an exercise for the reader to find the private key for those addresses.)

But how does the contract work? If you examine the winning transaction’s parameters (which uses 0x060000000084477daF071d5b34F36a028E8b4506 as the sender address), starting with the first case, here is what the stack looks like when the owner function is being called.

After the first four opcodes are executed, the stack looks like this:

Next, CALLDATALOAD consumes the 0x24 from the stack and pushes the 32 bytes of calldata starting at 0x24 onto the stack. Since the owner function only has four bytes of calldata, this action essentially pops 0x24 from the stack and replaces it with 0x00.

The next opcode, MSTORE consumes two elements from the stack, interpreting the top of the stack (0x00) as the memory location and the second item on the stack (the origin address) as the value to store. The next MSTORE opcode essentially acts as a NOP, as it stores 0x0900000000 at the memory location 0x24.

Finally, pushing MSIZE (0x60) and CALLVALUE (0x00) to the stack and then RETURN essentially returns these three words to the optimizer contract:

The first word is our origin address, while the rest is junk data. Fortunately, the optimizer contract only expects a single word back, and checks that it is equal to the original caller. Since we returned the origin address first, we can pass the first test.

Now, as we go into the solve function, things get a bit more complicated…

Like before, after the first four opcodes are executed, the stack looks like this:

This time, when we use CALLDATALOAD, we push the second element of the input array onto the stack. In the case of the winning transaction, this was 0x13. The next opcode, MSTORE then stores the origin address at the memory location 0x13. This is what the memory looks like at this point:

As you can see — because of the strange offset and origin address — the beginning 0x06 part of the address ends up as the first full word in memory. This was just a clever way to prepare our first return value, 0x06.

The next MSTORE stores the gas price (0x0900000000) at location 0x24. This operation therefore ends up covering memory locations 0x24 to 0x38 with zeros, and places 0x09 at location 0x39.

The rest of the zeros in the gas price overflow into the next word of memory, which expands the memory and sets 0x40 to 0x60 as all zeros. In effect, this MSTORE sets our second return value to 0x09 and our third one to 0x00.

At this point, our memory looks like this:

Next, MSIZE, CALLVALUE, and RETURN simply returns this data, and satisfies all the requirements of a proper solution (it has three values, all unique, and all between 0 and 9). If we’re lucky, the required sum happens to be equal to the sum of the three provided indexes. In our case, element 0 was 26, element 6 was 12, and element 9 was 15. Together they add up to 53, which was our desired sum, and so we “solved” it.

An argument can be made for why this solution may be difficult to beat – barring significant changes to the EVM.

Bold claim, but it gets at some underlying structural dynamics as well with Ethereum. To understand why, let’s look into the requirements of a valid solution.

1. We must supply at least 0x60 bytes (three words) of return data
2. All of these values must range between 0-9
3. All of these values must be unique
4. We must have a way to either change the logic between the owner() call and the solve(…) call or have an address between 0x01 and 0x09

We also need to understand some facts of the EVM.

1. MSTORE is at least as score (gas + opcode length) efficient at storing memory as all other operations (CALLDATACOPY, EXTCODECOPY, RETURNDATACOPY, and all calls) when operating on less than three words of memory
2. The cheapest way to put a value onto the stack is a two-cost operation (which will add three points to the score)
3. The most efficient logic operations cost three gas, and of those only CALLDATALOAD, NOT, and ISZERO have net-zero impact on the stack. All others consume more stack elements than they output
4. We must call RETURN at the end of the function
5. None of the precompiled addresses currently work to solve this problem

Since we must return three words of memory (two nonzero), we are required to have at least two MSTORE opcodes in the solution, and because we’re only setting two words, (1) above tells us the use of MSTORE here will be at least as efficient as other operations. This gives us the requirement of four stack pushes. We also need at least one RETURN opcode which requires another two stack pushes.

Finally, we need some way to differentiate between solve and owner calls, so there must be at least one logic operator to do so and, using (2) above, it follows that CALLDATALOAD is at least as efficient as any other logic operation. This means any solution needs at least twoMSTOREs, one RETURN, one efficient logic operation, and six stack pushing operations. Our solution uses two MSTOREs, one RETURN, one efficient logic operation, and the six cheapest stack pushing operations. All this amounts to our solution appearing to share the same characteristics as the optimal solution — it will at least tie every other solution.

Of course, this isn’t a formal proof, but it does give us confidence that our solution can’t technically be bested under current constraints. There is a trivially more efficient solution, but it requires something computationally infeasible: a private key for an address between 0x01 and 0x09. Since this is astronomically unlikely (and it’s the only method we know of) there’s not another way to win the NFT. (That is, in the absence of an EIP that would change the conditions.)

Building this was fun to say the least. Block builders are so new, and there is so much to uncover. For an even deeper dive, take a look at the block or the block builder that created it. There’s a whole lot going on (over two dozen transactions), but I promise every part of the block plays an important role.

***
The views expressed here are those of the individual AH Capital Management, L.L.C. (“a16z”) personnel quoted and are not the views of a16z or its affiliates. Certain information contained in here has been obtained from third-party sources, including from portfolio companies of funds managed by a16z. While taken from sources believed to be reliable, a16z has not independently verified such information and makes no representations about the current or enduring accuracy of the information or its appropriateness for a given situation. In addition, this content may include third-party advertisements; a16z has not reviewed such advertisements and does not endorse any advertising content contained therein.

This content is provided for informational purposes only, and should not be relied upon as legal, business, investment, or tax advice. You should consult your own advisers as to those matters. References to any securities or digital assets are for illustrative purposes only, and do not constitute an investment recommendation or offer to provide investment advisory services. Furthermore, this content is not directed at nor intended for use by any investors or prospective investors, and may not under any circumstances be relied upon when making a decision to invest in any fund managed by a16z. (An offering to invest in an a16z fund will be made only by the private placement memorandum, subscription agreement, and other relevant documentation of any such fund and should be read in their entirety.) Any investments or portfolio companies mentioned, referred to, or described are not representative of all investments in vehicles managed by a16z, and there can be no assurance that the investments will be profitable or that other investments made in the future will have similar characteristics or results. A list of investments made by funds managed by Andreessen Horowitz (excluding investments for which the issuer has not provided permission for a16z to disclose publicly as well as unannounced investments in publicly traded digital assets) is available at https://a16z.com/investments/.

Charts and graphs provided within are for informational purposes solely and should not be relied upon when making any investment decision. Past performance is not indicative of future results. The content speaks only as of the date indicated. Any projections, estimates, forecasts, targets, prospects, and/or opinions expressed in these materials are subject to change without notice and may differ or be contrary to opinions expressed by others. Please see https://a16z.com/disclosures for additional important information