Table of contents
- Why paying for “informed” voting is hard
- Voting with the majority
- The optimal mechanism for implementing informed voting
- The moral hazard problem
- The optimal mechanism
- An example
- Concerns with inducing informed voting
- Appendix
In our last piece, we showed how to design a mechanism that aims to get people to honestly report how costly they find it to vote and that then pays the subset of voters that find voting least costly to actually vote. But as many people have pointed out, incentivizing raw participation could lead to uninformed voting or bot voting in some circumstances.
Various projects and writers have proposed rewarding voters who vote in the majority and/or slashing voters who vote in the minority as a way to create incentives for informed voting. We thought it useful to do a formal analysis of the question. Here, we establish that while it is possible to incentivize informed participation this way, even in its optimal, most cost-effective form, doing so is likely to be prohibitively expensive. Moreover, the reward structure is somewhat more difficult to explain than one might hope, which could also be an impediment to implementation.
The reason for both of these challenges is an underlying moral hazard problem – whether people are actually informed is unobservable, so you need to make sure you aren’t simply incentivizing them to take a guess about how the majority will vote. As such, rewarding or slashing voters based on whether they vote in the majority or minority is probably not in general an effective approach. This finding may help with understanding the subtle effects of slashing addresses for voting against the majority (or, equivalently, rewarding addresses for voting in the majority) in other contexts, which will be the subject of future work.
Having shown the downsides to trying to pay directly for “informed” voting, we conclude by offering some concrete ideas for how projects can experiment with preventing the unproductive harvesting of voting rewards by bots or bad actors. In particular, projects can consider:
If all the project wants to do is incentivize voting, the direct revelation or ascending rewards implementation of the VCG mechanism does the job. But voting alone may not be sufficient to achieve the platform’s goals. It may want to incentivize some subset of voters to vote in an informed manner.
Incentivizing informed voting is harder than just incentivizing voting. It is almost surely impossible to know whether a voter in fact voted in an informed way – investment in information is largely unobservable. Some have suggested that voting with the majority might be an indication of having voted in an informed manner. The intuition is that members of a project often share substantial agreement about its goals. And, thus, we might think that if everyone did their homework, everyone would reach more or less the same conclusion about the right way to achieve those goals.
The first question, then, is whether we can incentivize informed voting by incentivizing voting with a majority.
Right off the bat, the way blockchain voting works creates a challenge. Currently, for most blockchain voting systems, votes are observable in real time. That is, if voter 2 votes after voter 1, voter 2 knows how voter 1 voted. This situation creates obvious problems of herding once we introduce incentives to vote with the majority — voters who vote later and want to win the reward will vote however the majority has voted, regardless of their own views on what the correct vote choice is.
But even if we assume we have access to a blockchain voting technology that obscures the voting results until after everyone has voted, we still face considerable challenges. Incentivizing informed voting based on voting with the majority:
Given these drawbacks, we think it is unlikely that projects in most cases can rely on rewarding voters for voting in the majority as a way to incentivize informed participation, even with an optimally designed incentive mechanism.
Suppose the platform wants n voters to vote and wants m≤n of them to vote in an informed manner. Each token holder has two different costs: their cost of voting (ci) and their cost of gathering information (ki).
To keep things simple, we make four assumptions.
The platform sorts token holders into three groups:
The mechanism has to sort token holders into groups and choose payments to achieve two goals as cost effectively as possible. First, it has to get the token holders to truthfully reveal their costs. Second, it has to incentivize token holders to behave as desired (so members of V vote and members of I vote informed).
Start by thinking about the optimal mechanism if becoming informed was observable, so that the payment pI was conditional on actually voting informed, as opposed to on voting with the majority. (This would be a slightly more involved version of the VCG problem we discussed in our first post.) To keep costs as low as possible, the mechanism would put the lowest cost token holders (1 through m) in group I and the next lowest cost token holders (m + 1 through n) in group V, as illustrated in Figure 1. And, just as in our earlier post, to make token holders want to truthfully reveal their costs, the mechanism would offer each token holder a payment equal to their externality – that is, the effect of their presence on the aggregate welfare of everyone other than themselves. Let’s see what those payments are.
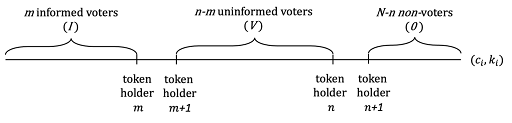
Figure 1. Dividing token holders into three groups: the lowest cost token holders become informed voters (I), the next lowest cost become uninformed voters (V), and the remainder become non-voters (O).
What is the externality of a token holder in group V? If that token holder were removed, to get the number of voters back up to n, voter n + 1 would have to vote at cost cn+1; this is the effect of any voter in group V on aggregate welfare. Thus, the payment offered to members of group V would be pV = cn+1 . This is illustrated in Figure 2.

Figure 2. If an uninformed voter were eliminated, to keep n token holder n + 1 would have to be moved into the uninformed voting group, bearing voting cost cn+1.
What is the externality of a token holder in group I? If that token holder were removed, to get the number of voters voting informed back up to m, voter m + 1 would have to be moved into group I and vote informed. This voter is already bearing the costs of voting, but now also must bear the costs of becoming informed, at cost km+1. Additionally, we would also need to add a new member to group V to get the number of voters back up to n. This would be voter n + 1, who has to vote at cost cn+1. Thus, the total effect of a token holder in group I on aggregate welfare of other token holders is cn+1 + km+1 , so this is the payment they would each be offered, pI = cn+1 + km+1. This is illustrated in Figure 3.
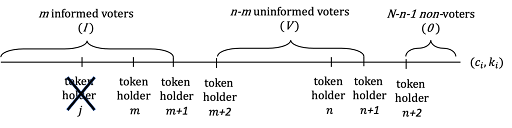
Figure 3. If an informed voter were eliminated, to keep m informed voters, token holder m + 1 would have to be moved into the informed voting group, bearing additional information costs of km+1. Moreover, token holder n + 1 would have to be moved into the uninformed voting group to keep n total voters, bearing voting cost cn+1.
If the mechanism could condition payments directly on how token holders behave — that is, if becoming informed was observable — this would be the whole answer. As we show in the appendix, these payments induce truth telling by the token holders. And there is no cheaper way to do so.
The analysis above is not implementable because we can’t actually observe whether a token holder in group I voted in an informed manner so we can’t make payment conditional on becoming informed. This is why people have been interested in the idea of conditioning the payment pI on voting with the majority of I — given our assumption that informed voters learn the truth perfectly, if everyone else in I votes informed a member of I can guarantee themselves payment by becoming informed. So paying people to vote with the majority provides them with incentives to invest in information.
But such incentives aren’t as strong as the incentives created above, where we assumed we could actually observe whether voters become informed. This is because of the moral hazard problem created by unobservability. If voters are rewarded based on voting with a majority, they can become informed and (assuming others also become informed) guarantee themselves payment. But they can also not become informed and take a guess about how the majority will vote. If they guess right, they still get paid, while avoiding the costs of acquiring information.
This option weakens the incentives for the members of group I to invest in information. Moreover, it creates another complication. If the payment to group I is too generous relative to the payment to group V, token holders who should be in group V might have an incentive to understate their costs, get themselves assigned to group I, and vote uninformed in the hopes of guessing correctly. To fully characterize the optimal mechanism, we have to take these moral hazard concerns into account.
To analyze this question, we have to ask how likely a token holder is to guess correctly, voting with a majority of I even if they don’t become informed. Suppose all the other members of I become informed. Then, with probability q > ½ they will all vote for A and with probability q < ½ they will all vote for B. That means that an uninformed token holder’s best guess is A and they guess correctly with probability q. Thus, a voter i in group I who takes their best guess makes an expected payoff of q · pI – ci.
There is a subtlety here that is worth pointing out. We’ve changed the question about implementability in an important way. The VCG asks whether the desired behavior can be implemented as a weakly dominant strategy — that is, token holders want to behave as desired regardless of what everyone else does. Such dominance implementability is no longer possible once we make payments conditional on voting with a majority, since getting paid depends on how all others vote. So now we are asking whether the outcome we desire is weakly implementable. Does a Nash equilibrium exist in which agents behave as we want? As we’ll discuss below, even when the answer is yes, there are other Nash equilibria too.
First, consider a token holder who should be assigned to group V. If that token holder tells the truth, they get put in group V and make a payoff of pV – ci. If they instead lie to get into group I and take their best guess, they make a payoff of q · pI – ci. Comparing, this token holder will tell the truth about their costs if:
pV ≥ q · pI.
Second, consider a token holder who will be assigned to group I. If that token holder becomes informed, they make a payoff of pI – ci – ki. If they don’t become informed and take their best guess, they make a payoff of q · pI – ci. Comparing, this token holder will become informed if:
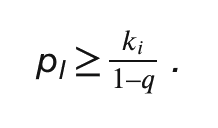
The analysis above gives us four constraints that must be satisfied to induce truth telling and correct behavior. They are:
pV ≥ cn+1
pV ≥ q · pI
pI ≥ cn+1 + km+1

The last of these constraints is hardest to fulfill for the highest cost token holder in group I, token holder m. And, of course, m’s payment can’t depend directly on her cost because then she’ll have an incentive to overstate that cost. Thus, the cheapest way we can fulfill the final constraint while inducing truth telling is with
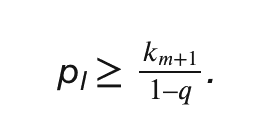
This now gives us a complete characterization of the optimal mechanism. We have
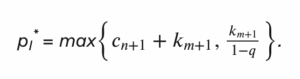
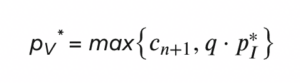
Note that pI* and pV* can each take one of two values. Which they take depends on q and on the relative values of cn+1 and km+1, in a way we state precisely in the appendix. But, as shown in Figure 4, the basic shape of the payoffs as a function of q is always the same.
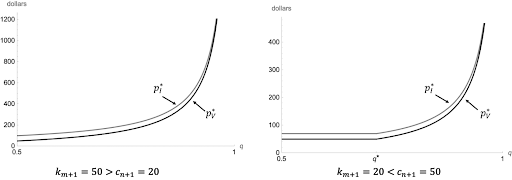
Figure 4. The optimal payments to both groups as a function of q for two different values of cn+1and km+1.
To illustrate the mechanism, let’s think about an example. Suppose there are five token holders, each of whom holds 1 token, with costs as follows.
| Token Holder | Cost of voting (ci) | Cost of information (ki) |
| 1 | $2 | $3 |
| 2 | $4 | $5 |
| 3 | $9 | $11 |
| 4 | $12 | $14 |
| 5 | $14 | $15 |
The project wants to get n=3 people to vote and wants at least m=2 of them to vote in an informed way. Moreover, suppose the project thinks the probability that A is the right choice is q=.6.
The project asks each token holder to reveal their costs and the token holders do so. The platform finds the following two numbers: cn+1=4 = $12 and km+1=3 = $11.
Our mechanism then chooses:
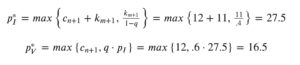
Token holders 1 and 2 are assigned to group I, vote informed, and are paid $27.5 each because they vote the same and end up in the majority. Token holder 3 is assigned to group V, votes uninformed, and is paid $16.5.
We have characterized the optimal mechanism for incentivizing informed voting by paying people to vote with a majority. Three features of this mechanism highlight some real concerns with the feasibility of actually implementing such incentives.
The first is that providing the right incentives can be quite expensive. In our example, the total cost of voting and information borne by token holders is $23 (token holders 1 and 2 bear the costs of voting and information, token holder 3 only bears the cost of voting). Yet total compensation paid out by the mechanism is $71.5 (token holders 1 and 2 each receive $27.5 while token holder 3 receives $16.5). Unfortunately, because the platform doesn’t know the voters’ costs, there isn’t a cheaper way to achieve the goal.
More generally, the total cost of inducing m informed votes and n total votes is
Total Cost = m · pI* + (n – m) · pV*.
This total cost depends on three things:
The platform’s costs are increasing linearly in m, n – m, cn+1, and km+1. But as Figure 4 illustrates, they are increasing hyperbolically in q. Moreover, as q gets close to 1, so there is essentially no uncertainty about the correct choice, the cost of inducing informed voting goes to infinity. This is because, if A is almost certain to be the correct option, there is no reason for token holders in group I to invest in becoming informed. They can just vote A and almost certainly be in the majority anyway. Thus, it is probably only feasible to consider buying informed votes when there is substantial uncertainty about the correct choice – that is, when q is close to one-half. Fortunately, this is also presumably the circumstance where informed voting is most valuable.
A second concern is that the mechanism may be somewhat difficult for token holders to understand — although the requirements of the token holders may be less taxing than the mathematics suggest. Token holders need to be able to (1) state their own personal costs of voting and of getting information and (2) upon being given a simple contract, be able to understand the direction of their monetary incentives.
The third concern is more fundamental. Any incentive scheme that works based on whether voters vote with the majority in their group is subject to concerns about coordination problems. That is, the analysis above shows that it is an equilibrium for all token holders to behave as described. But there is always another equilibrium.
Imagine a token holder in group I believes that no other token holder in group I is going to invest in information. Then that token holder believes that knowing the right option will not help them vote with the majority of group I, since the majority vote will not be determined by what the right option is. As such, that token holder has no incentive to invest in information. Thus, under an incentive scheme that pays people to vote with the majority of group I, in addition to the good “informed” equilibrium, there is also always a bad “uninformed” equilibrium in which no token holder invests in information because they (correctly) believe other token holders won’t invest in information.
***
Our takeaway from these analyses is that rewarding or slashing voters based on whether they vote in the majority or minority is not the most promising way to reward voting while discouraging uninformed voting or bot voting.
For projects that think the basic rewards mechanism is too vulnerable to gaming or uninformed voting, a logical way to start is by only offering rewards to addresses with some kind of track record of contributions to the project. This would be in line with recent experiments in retroactive rewards, such as Optimism’s ongoing work.
Separately or in addition, projects could also explore staking requirements that only provide rewards to addresses that are locked into the protocol for long periods of time, to disincentivize short-term voting rewards harvesting.
***
Ethan Bueno de Mesquita is the Sydney Stein Professor at the Harris School of Public Policy at the University of Chicago. His research focuses on applications of game theoretic models to a variety of political phenomena. He advises tech companies and others on governance and related issues.
Andrew Hall is a Professor of Political Economy in the Graduate School of Business at Stanford University and a Professor of Political Science. He works with the a16z research lab and is an advisor to tech companies, startups, and blockchain protocols on issues at the intersection of technology, governance, and society.
***
Editor: Tim Sullivan
***
If becoming informed was observable, then pV = cn+1 and pI = cn+1 + km+1 induces truth telling.
First, note that everyone would be happy to participate in this mechanism. Each token holder that will end up in group V makes a payoff of pV – ci. Since pV = cn+1 and the members of group V all have costs ci < cn+1, they are making positive payoffs. Similarly, each token holder in group I would make a payoff of pI – ci – ki. Since pI = cn+1 + km+1 and the members of group I all have costs ci < cn+1 and ki < km+1, they too are making positive payoffs.
Second, it is weakly dominant to tell the truth for all token holders.
If a member of group V claimed a higher cost, either there would be no change to their payoff or they would be assigned to group O and make 0. If a member of group V claimed a lower cost, either there would be no change to their payoff or they would be assigned to group I. In that case, they’d make a payoff of cn+1 + km+1 – ci – ki. But since members of group V have costs of information ki ≥ km+1, this is worse than their payoff from being in group V.
If a member of group I claimed a lower cost, they’d still be in group I, so they’d make the same payoff. If they claimed a higher cost, either there would be no change to their payoff (if they stayed in group I) or they would be assigned to group O and make 0 (obviously not profitable), or they’d be assigned to group V. In that event they’d make a payoff of cn+1 – ci. But since members of group I have costs of information ki < km+1, this is worse than their payoff from being in group I.
In the text we showed
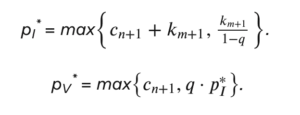
From this, it is straightforward that:
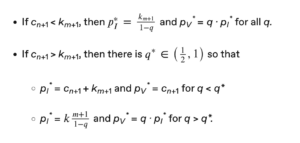
***
The views expressed here are those of the individual AH Capital Management, L.L.C. (“a16z”) personnel quoted and are not the views of a16z or its affiliates. Certain information contained in here has been obtained from third-party sources, including from portfolio companies of funds managed by a16z. While taken from sources believed to be reliable, a16z has not independently verified such information and makes no representations about the enduring accuracy of the information or its appropriateness for a given situation. In addition, this content may include third-party advertisements; a16z has not reviewed such advertisements and does not endorse any advertising content contained therein.
This content is provided for informational purposes only, and should not be relied upon as legal, business, investment, or tax advice. You should consult your own advisers as to those matters. References to any securities or digital assets are for illustrative purposes only, and do not constitute an investment recommendation or offer to provide investment advisory services. Furthermore, this content is not directed at nor intended for use by any investors or prospective investors, and may not under any circumstances be relied upon when making a decision to invest in any fund managed by a16z. (An offering to invest in an a16z fund will be made only by the private placement memorandum, subscription agreement, and other relevant documentation of any such fund and should be read in their entirety.) Any investments or portfolio companies mentioned, referred to, or described are not representative of all investments in vehicles managed by a16z, and there can be no assurance that the investments will be profitable or that other investments made in the future will have similar characteristics or results. A list of investments made by funds managed by Andreessen Horowitz (excluding investments for which the issuer has not provided permission for a16z to disclose publicly as well as unannounced investments in publicly traded digital assets) is available at https://a16z.com/investments/.
Charts and graphs provided within are for informational purposes solely and should not be relied upon when making any investment decision. Past performance is not indicative of future results. The content speaks only as of the date indicated. Any projections, estimates, forecasts, targets, prospects, and/or opinions expressed in these materials are subject to change without notice and may differ or be contrary to opinions expressed by others. Please see https://a16z.com/disclosures for additional important information.