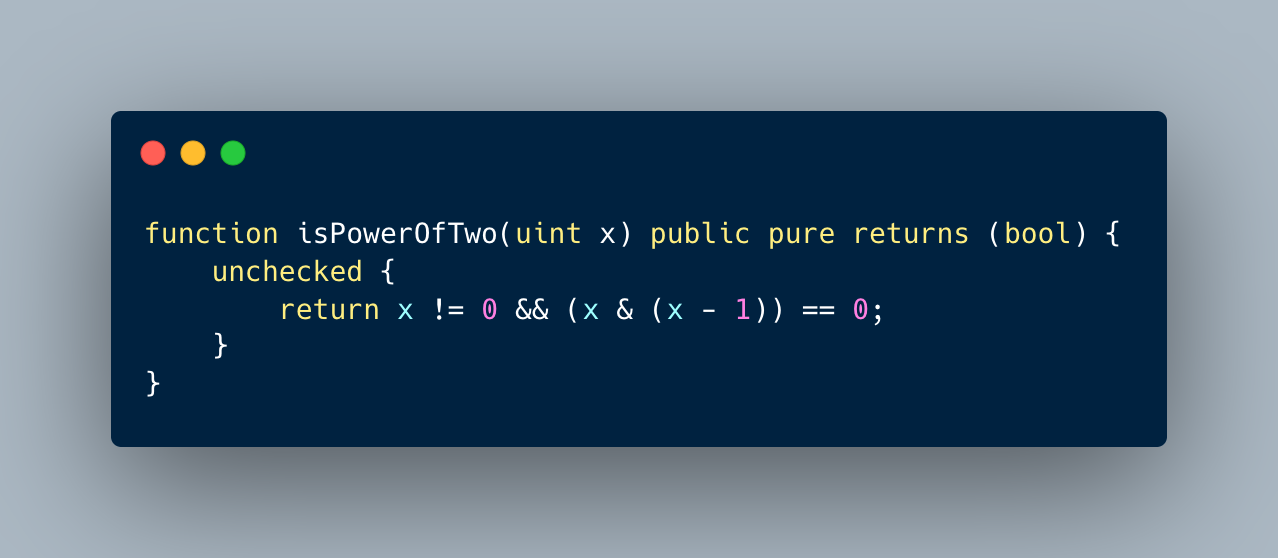
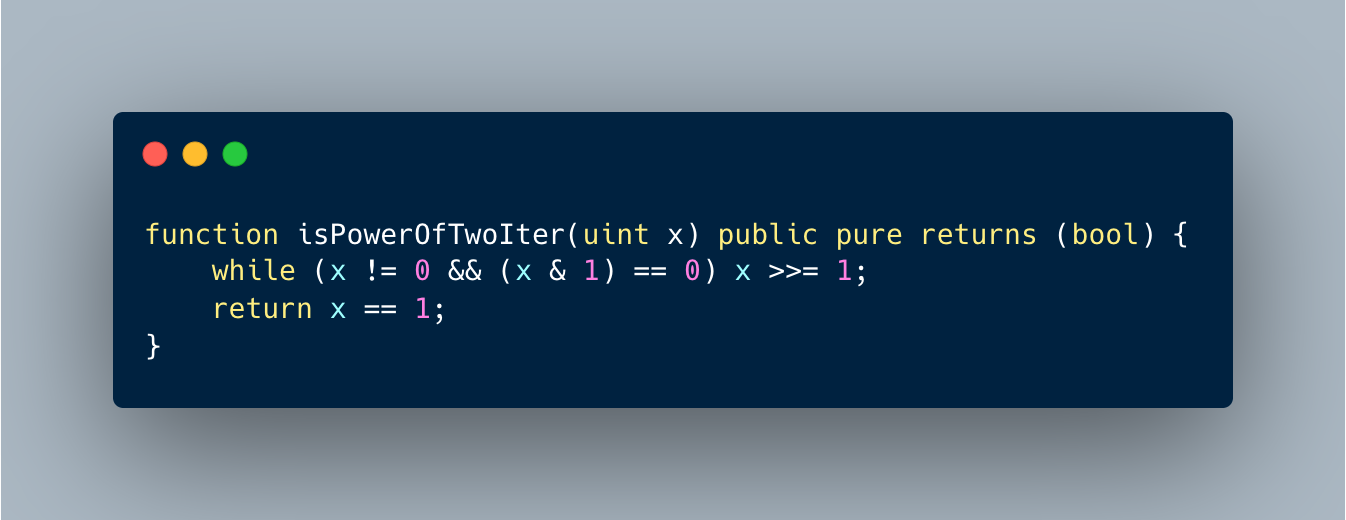
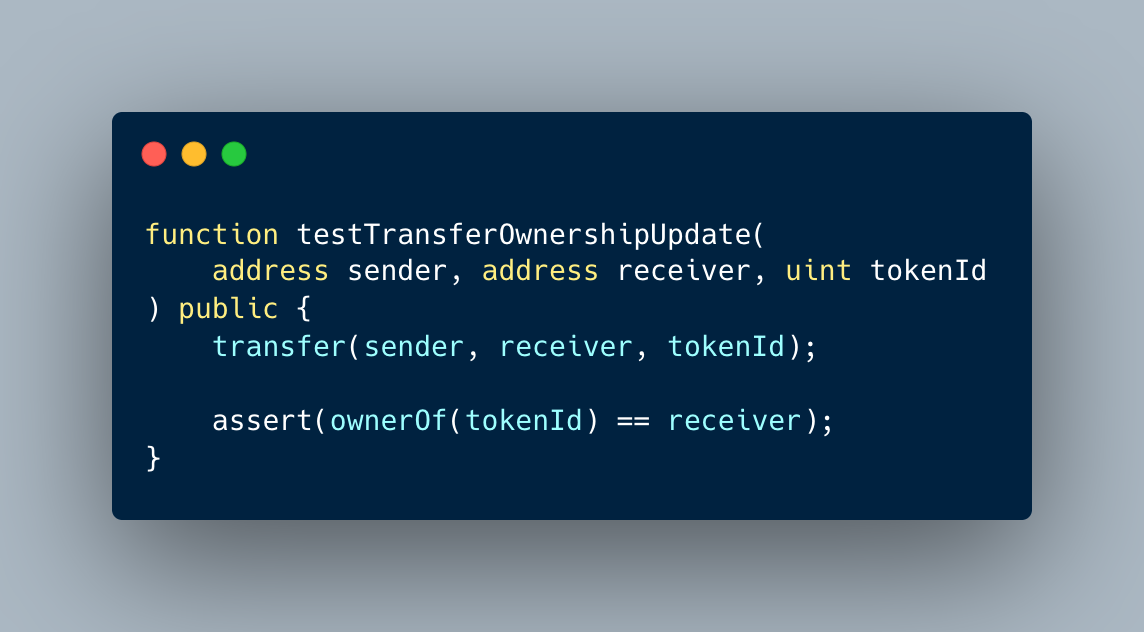
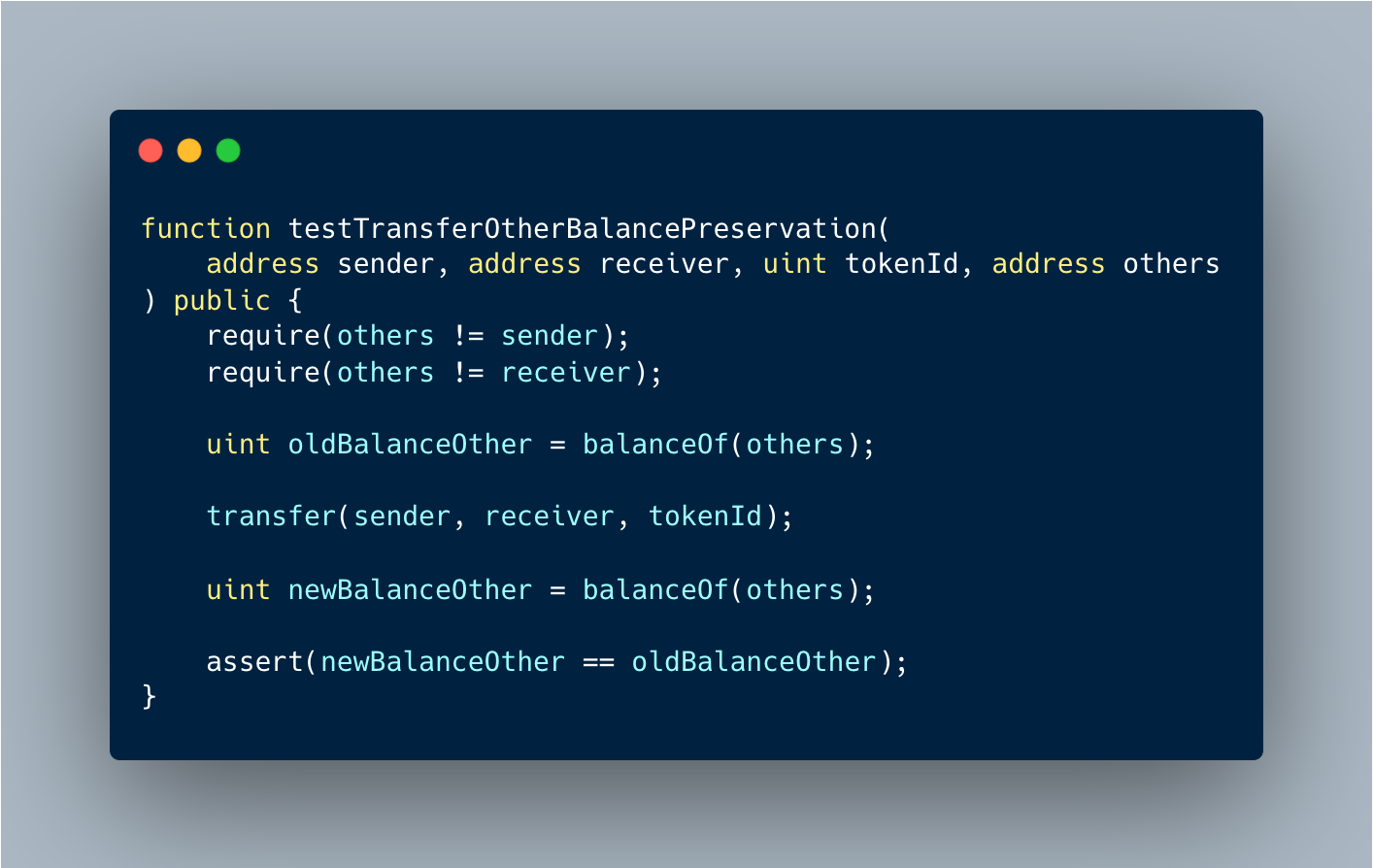
Formal verification tools for Ethereum smart contract bytecode have been developed by various teams. These tools, including Halmos, can be used to help ensure the security and correctness of smart contracts. Comparing and understanding the different features, capabilities, and limitations of these tools can help developers choose the most appropriate one for their unique needs.
While Halmos is a valuable addition to the toolset available for smart contract verification, it is meant to complement (not replace) existing tools. Developers can combine Halmos with other tools to achieve a higher level of assurance in their contracts. Below, we compare Halmos with a few selected formal tools that support EVM bytecode.
- K is a powerful formal verification framework that enables deductive verification and interactive theorem proving. Its underlying theory and implementation provide a high level of expressiveness, making it suitable for verifying complex programs and algorithms. However, it should be noted that K is not designed with heavy emphasis on automated verification and lacks certain automation features which can require more manual effort during the verification process. To use the K framework, formal specifications are written in the K language, which must be learned prior to use. Its strength is particularly useful in verifying complex systems, which may be challenging to analyze using automated reasoning.
- Certora is a formal verification tool for smart contracts that focuses on automated verification and supports bounded model checking, similar to Halmos. To use Certora, developers must learn their new language, CVL, in order to write specifications. This language allows for the concise description of many critical properties through contract invariants, a feature that Halmos currently does not support. Despite being a closed-source, proprietary tool, Certora provides robust formal verification tooling, with ongoing development and good user support.
Halmos, on the other hand, is an open-source tool that is smaller in scale and currently lacks some features provided by Certora, but it is meant to serve as a public good and is intended as a niche solution for quickly verifying smart contracts without the need for extensive setup and maintenance.
- HEVM is another formal verification tool that is similar to Halmos. It was previously part of DappTools, which is a precursor of Foundry. Both HEVM and Halmos have the feature of not requiring a separate specification and can symbolically execute existing tests to identify assertion violations. This allows users to use both tools interchangeably or run them in parallel for the same tests, providing them with multiple options for symbolic testing.
It’s worth noting that, despite their similarities, HEVM and Halmos have been independently developed and differ in their implementation details; particularly in terms of optimizations and symbolic reasoning strategies. Additionally, HEVM is written in Haskell, while Halmos is written in Python, providing exposure to the rich Python ecosystem. Having the ability to use both tools gives users more flexibility and options to ensure the security and correctness of smart contracts.
Halmos is open source, and currently in its beta phase. We are actively working on new features and functionality, including Foundry cheat codes and several other key usability features. We would greatly appreciate your thoughts on which features are most important, and welcome any feedback, suggestions, and contributions to make Halmos a better tool for everyone.
**
The views expressed here are those of the individual AH Capital Management, L.L.C. (“a16z”) personnel quoted and are not the views of a16z or its affiliates. Certain information contained in here has been obtained from third-party sources, including from portfolio companies of funds managed by a16z. While taken from sources believed to be reliable, a16z has not independently verified such information and makes no representations about the current or enduring accuracy of the information or its appropriateness for a given situation. In addition, this content may include third-party advertisements; a16z has not reviewed such advertisements and does not endorse any advertising content contained therein.
This content is provided for informational purposes only, and should not be relied upon as legal, business, investment, or tax advice. You should consult your own advisers as to those matters. References to any securities or digital assets are for illustrative purposes only, and do not constitute an investment recommendation or offer to provide investment advisory services. Furthermore, this content is not directed at nor intended for use by any investors or prospective investors, and may not under any circumstances be relied upon when making a decision to invest in any fund managed by a16z. (An offering to invest in an a16z fund will be made only by the private placement memorandum, subscription agreement, and other relevant documentation of any such fund and should be read in their entirety.) Any investments or portfolio companies mentioned, referred to, or described are not representative of all investments in vehicles managed by a16z, and there can be no assurance that the investments will be profitable or that other investments made in the future will have similar characteristics or results. A list of investments made by funds managed by Andreessen Horowitz (excluding investments for which the issuer has not provided permission for a16z to disclose publicly as well as unannounced investments in publicly traded digital assets) is available at https://a16z.com/investments/.
Charts and graphs provided within are for informational purposes solely and should not be relied upon when making any investment decision. Past performance is not indicative of future results. The content speaks only as of the date indicated. Any projections, estimates, forecasts, targets, prospects, and/or opinions expressed in these materials are subject to change without notice and may differ or be contrary to opinions expressed by others. Please see https://a16z.com/disclosures for additional important information.