On-Chain Trusted Setup Ceremony

The trusted setup ceremony is one of the pains — and excitements — of crypto communities. The goal of a ceremony is to generate trustworthy cryptographic keys for securing crypto wallets, blockchain protocols, or zero-knowledge proof systems. These (sometimes flamboyant) procedures are frequently the root of trust for a given project’s security, and they are therefore extremely important to get right.

Blockchain projects run ceremonies in numerous creative ways — involving blowtorches, radioactive dust, and airplanes – but all share something in common: they all involve a centralized coordinator. With this work we demonstrate how to decentralize the process by replacing the centralized coordinator with a smart contract. In addition, we’re open-sourcing a library that allows anyone to run such a ceremony — known to crypto practitioners as a Kate-Zaverucha-Goldberg (KZG) or “powers-of-tau” ceremony — on the Ethereum chain. Anyone can participate simply by paying the transaction fees!

Our decentralized approach has limitations, but it’s still useful. Due to current on-chain data constraints, the size of the cryptographic parameters has to be kept short, i.e. no more than 64 KB. But the number of participants has no cap and people can keep submitting contributions in perpetuity. Applications for these short parameters include small zero-knowledge SNARKs, data-availability sampling, and Verkle trees.

In a typical trusted setup ceremony, a group of participants will collaboratively generate a set of cryptographic parameters. Each participating party uses secret information, generated locally, to generate data that helps create these parameters. Proper setups ensure secrets do not leak, that secrets are only used as designated by the protocol, and that these secrets are completely destroyed at the end of the ceremony. As long as at least one party in the ceremony behaves honestly, is not compromised, and destroys its local secret, the entire setup can be considered secure. (Of course, that is assuming the math is correct and the code has no bugs.)

Some of the most prominent ceremonies were run by Zcash, a privacy-oriented blockchain project. Participants in these ceremonies generated public parameters designed to allow Zcash users to construct and verify private crypto transactions. Six participants carried out the first Zcash ceremony, Sprout, in 2016. Two years later, crypto researcher Ariel Gabizon, now a Chief Scientist at Aztec, found a devastating bug in the design of the ceremony which was inherited from a foundational research paper. The vulnerability could have enabled attackers to create unlimited Zcash coins without being detected. The Zcash team kept the vulnerability secret for seven months until a system upgrade, Sapling, whose ceremony involved 90 participants, addressed the issue. While an attack based on the security hole would not have affected the privacy of users’ transactions, the prospect of infinite counterfeiting undermined Zcash’s security premise. (It’s theoretically impossible to know whether an attack took place.)

Another notable example of a trusted setup is the perpetual “powers-of-tau” ceremony designed primarily for Semaphore, a privacy preserving technology for anonymous signaling on Ethereum. The setup used a BN254 elliptic curve and has had 71 participants so far. Other prominent projects later used this setup to run their own ceremonies on top, including Tornado.Cash (recently sanctioned by the U.S. government), Hermez network, and Loopring. Aztec coordinated a similar ceremony on a BN254 curve to create a universal common reference string (CRS) for use by PLONK zk-snarks. zkSync, a “layer two” Ethereum scaling solution, participated in the ceremony and uses this CRS to underpin the security of their zero knowledge rollup. Filecoin, a decentralized data storage protocol, ran a ceremony with 19 and 33 participants, in first and second phase respectively, forking the original repo. Celo, a layer-1 blockchain, ran a ceremony for their light-client Plumo too.

Perpetual ceremonies have no limit to the number of participants. In other words, instead of trusting other people to run a trusted setup ceremony, ANYONE can participate to whatever degree of security meets their satisfaction. A single trustworthy participant ensures the security of all of the resulting parameters; the chain is as strong as its strongest link. Perpetual ceremonies may run, as the name implies, in perpetuity, as was the premise with the original powers-of-tau ceremony. That said, projects often decide on a concrete beginning and end time for their ceremonies, that way they can embed the resulting parameters into their protocols and don’t have to worry about continually updating them.

Ethereum plans to run a smaller trusted setup ceremony for upcoming ProtoDankSharding and DankSharding upgrades. Those two upgrades will increase the amount of data that the Ethereum chain provides to clients for storage. This data will have an expiry of suggested 30-to-60 days. The ceremony is under active development, and is planned to run for six weeks early next year. (See kzg-ceremony-specs for more details.) It’s shaping up to be the largest trusted setup ceremony for blockchains run so far.

Paranoia is a virtue when it comes to trusted setup ceremonies. If a machine’s hardware or software is compromised, that can undermine the security of the secrets it generates. Sneaky side channel attacks which leak secrets can also be difficult to rule out. A phone can spy on a computer’s operations by recording sound waves of CPU vibrations, for example. In practice, since it is immensely hard to eliminate all possible side channel attacks – including those still to be discovered or disclosed – there are even proposals to fly machines to space to conduct ceremonies there.

For now, the playbook for serious ceremony participants typically goes as follows. Buy a new machine (untainted hardware). Air-gap it by removing all the network cards (to prevent local secrets from leaving the machine). Run the machine in a Faraday cage at a remote undisclosed location (to foil would-be snoopers). Seed the pseudo-random secret generator with lots of entropy and hard-replicate data such as random key-strokes or video files (to make the secrets hard to crack). And finally, destroy the machine – along with any traces of the secrets – by burning everything to ashes. 😀

Here is a fun selection of quotes from some previous trusted setup ceremony participants:

• “…the blowtorch was used to methodically heat the electronics completely piece by piece until everything was blackened…” — Peter Todd on physically destroying the local secrets.
• “I have here a piece of fabric that has graphite dust [from] the core of the [Chernobyl] reactor… You count every four pulses [from a Geiger counter hooked up to a microcontroller] and you compare the time interval between pulse one and two and the time interval between pulse three and four and if it’s greater you get a zero, if it’s less you get a one.” “…we are about to get in this airplane and generate our random numbers…” — Ryan Pierce and Andrew Miller on secret generation.

Zcash powers-of-tau ceremony round 41 involved an airplane. Screenshot: YouTube video

• “The salesperson said they had 13 [computers]. I asked if we could pick one of the 13. He asked if there was something I was looking for in particular (confused because they are all the same) and I said I just wanted to pick a random one. He said he could not let us into the back warehouse. I asked if he would bring two of them out so we could pick one of the two. He brought two out on a handcart. Jerry selected one of the two computers and we took that to the register to check out.” — Peter Van Valkenburgh on getting a new machine.
• “The first few hours of the ceremony were performed in a makeshift Faraday cage made of aluminium foil and cling wrap. I moved the laptop out of the Faraday cage as it had poor ventilation and was getting hot to the touch” — Koh Wei Jie on side-channel protection.
• “.. performed one part of ceremony in the mountains with no neighbors.” — Micheal Lapinski on side-channel protection.
• ”I opted to use video of the surroundings to generate sufficient entropy” — Muhd Amrullah on generation of random values.

Za Wilcox, brother of Zcash cofounder Zooko Wilcox, destroying a computer used to generate random numbers for a trusted ceremony in 2016. Photo: Morgen Peck

All of these ceremonies relied on a centralized coordinator. The coordinator is an individual or private server or some other entity who is entrusted to register and order participants, to act as a relay by forwarding information from the previous participant to the next, and to keep a centralized log of all communications for auditability purposes. The coordinator is typically also in charge of making the log available to the public in perpetuity; of course, it’s always a possibility with a centralized system for data to get lost or mismanaged. (Perpetual-powers-of-tau for example is stored on Microsoft Azure and Github.)

It struck us as ironic that crypto projects must rely on centralized trusted setup ceremonies when decentralization is such a core tenet of the crypto ethos. So we decided to demonstrate the feasibility of running a small ceremony for perpetual-powers-of-tau directly on the Ethereum blockchain! The setup is fully decentralized, permissionless, censorship resistant, and is secure as long as any single one of the participants is honest [see disclaimers]. Participating in the ceremony costs only 292,600 to 17,760,000 gas (about $7 to $400 at current prices), depending on the size of the desired resulting parameters (in this case between 8 and 1024 powers-of-tau). (See the Table below for concrete costs – we go into more detail about these calculations later in the post.)

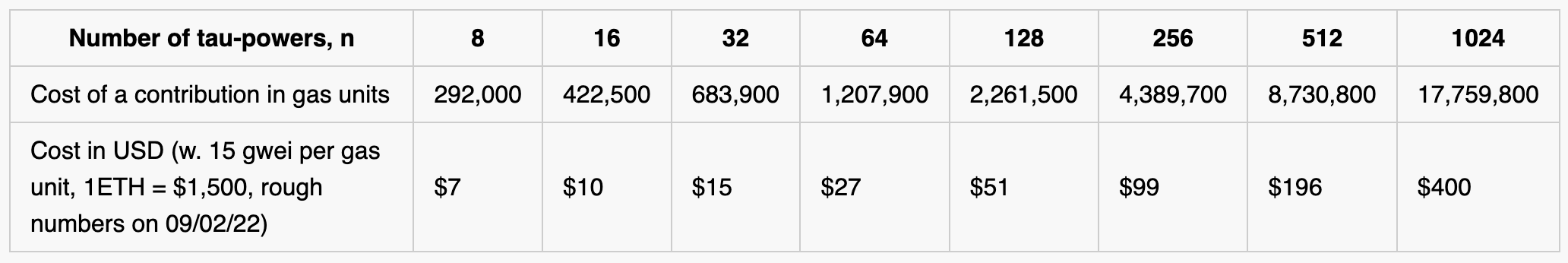
As yet, we advise not to use the code for anything other than experimental purposes! We would greatly appreciate it if anyone who finds any issues with the code reports them to us. We would love to collect feedback on and audits of our approach.

Let’s explore one of the most popular trusted setups, which is known as the KZG, or “powers-of-tau,” ceremony. Credit to Ethereum cofounder Vitalik Buterin, whose blog post on trusted setups informed our ideas in this section. The setup generates the encodings of the powers-of-tau, so named because “tau” happens to be the variable used to express the secrets generated by participants:

pp = [[𝜏]₁, [𝜏²]₁, [𝜏³]₁, …, [𝜏ⁿ]₁;    [𝜏]₂, [𝜏²]₂, …, [𝜏^k]₂]

For some applications (e.g. Groth16, a popular zkSNARK proving scheme designed by Jens Groth in 2016), this first-phase of the setup is followed by a second phase, a multiparty computation (MPC) ceremony, that generates parameters for a specific SNARK circuit. However, our work focuses solely on phase one. This first phase – the generation of the powers-of-tau – is already useful as a foundational building block for universal SNARKs (e.g. PLONK and SONIC), as well as other cryptography applications, such as KZG commitments, Verkle trees and data-availability sampling (DAS). Generally, universal SNARK parameters should be very large so they can support big and useful circuits. Circuits that contain more gates are generally more useful as they can capture large computations; the number of powers-of-tau roughly corresponds to the number of gates in the circuit. So, a typical setup will be of size |pp| = ~40 GB and capable of supporting circuits with ~2²⁸ gates. Given Ethereum’s current constraints, it would be infeasible to put such large parameters on-chain, but a smaller trusted setup ceremony useful for small SNARK circuits, Verkle trees, or DAS can feasibly be run on-chain.

The Ethereum Foundation is planning to run several smaller ceremonies for powers-of-tau of size 200 KB to 1.5 MB. While bigger ceremonies may seem better, given that larger parameters can create more useful SNARK circuits, bigger is, in fact, not always better. Certain applications, such as DAS, specifically need a smaller one! [The reason is very technical, but if you’re curious, it’s because a setup with n powers (in G₁) only enables KZG-commitments to polynomials of degree ≤ n, which is crucial for making sure that the polynomial underneath the KZG-commitment can be reconstructed from any n evaluations. This property enables data-availability-sampling: every-time t random evaluations of the polynomial are successfully obtained (sampled) it gives an assurance that the polynomial can be fully-reconstructed with probability t/n. If you want to learn more about DAS, check out this post by Buterin on the Ethereum Research forum.]

We designed a smart contract that can be deployed on the Ethereum blockchain to run a trusted setup ceremony. The contract stores the public parameters – the powers-of-tau – fully on-chain, and collects participation through users’ transactions.

A new participant first reads those parameters:

pp₀ = ([𝜏]₁, [𝜏²]₁, [𝜏³]₁, …, [𝜏ⁿ]₁;    [𝜏]₂, [𝜏²]₂, …, [𝜏^k]₂),

then samples a random secret 𝜏’ and computes updated parameters:

pp₁ = ([𝜏𝜏’]₁, [(𝜏𝜏’)²]₁, [(𝜏𝜏’)³]₁, …, [(𝜏𝜏’)ⁿ]₁;    [𝜏𝜏’]₂, [(𝜏𝜏’)²]₂, …, [(𝜏𝜏’)^k]₂),

and publishes them on-chain with a proof that demonstrates three things:

1. Knowledge of discrete-log: the participant knows 𝜏’. (A proof that the latest contribution to the trusted setup ceremony builds on the work of all preceding participants.)
2. Well-formedness of the pp₁: the elements indeed encode incremental powers.(A validation of the well-formedness of a new participant’s contribution to the ceremony.)
3. The update is not-erasing: 𝜏’ ≠ 0. (A defense against attackers trying to undermine the system by deleting all participants’ past work.)

The smart contract verifies the proof and if it is correct, it updates the public parameters that it stores. You can find more details on the math and the reasoning behind it in the repo.

The main challenge of running the setup on-chain is making the trusted setup ceremony as gas-efficient as possible. Ideally, submitting a contribution would cost no more than ~$50. (Large projects might be able to subsidize gas for contributors, in which case having hundreds of participants each spending $100 is easier to imagine). Below, we give more details on the most expensive parts of the setup. Lower gas costs would reduce the cost of contributions and allow for the construction of longer parameters (more tau-powers and bigger SNARK circuits)!

Our setup works for the elliptic curve BN254 (also known as BN256, BN128, and alt_bn128), that has support for the following precompiled contracts on Ethereum:

• ECADD allows two elliptic curve points to be added, i.e. compute [𝛼+𝛽]₁ from [𝛼]₁ and [𝛽]₁: gas cost 150
• ECMULT allows elliptic curve points to multiplied by a scalar, i.e. compute [a*𝛼]₁ from a and [𝛼]₁: gas cost 6,000
• ECPAIR allows a product of elliptic curve pairings to be checked, i.e. compute e([𝛼₁]₁, [𝛽₁]₂)* … *e([𝛼₁]₁, [𝛽₁]₂) = 1 which is equivalent to checking that 𝛼₁*𝛽₁+ … + 𝛼_k*𝛽_k = 0 : gas cost 34,000 * k + 45,000

Might Ethereum enable BLS12_381 (as proposed in EIP-2537), our setup contract could be easily made to work for this other curve as well.

Let’s estimate the gas cost to update the setup to ([𝜏]₁, [𝜏²]₁, [𝜏³]₁, …, [𝜏ⁿ]₁;    [𝜏]₂):

1. Gas cost of verifying the proof. Each participant updates the setup and submits a proof with three components as described above. The components 1 and 3 of the proof – “knowledge of discrete log” and “update being non-erasing” – are very cheap to verify. The challenge is in verifying component 2, “well-formedness of the pp₁”, on chain. It requires a large multi-scalar-multiplication (MSM) and two pairings:
   e(𝝆₀[1]₁ + 𝝆₁[𝜏]₁ + 𝝆₂[𝜏²]₁ + … + 𝝆_n-1[𝜏^n-2]₁, [𝜏]₂) = e([𝜏]₁ + 𝝆₁[𝜏²]₁ + … + 𝝆_n-1[𝜏^n-1]₁, [1]₂),
   where 𝝆₀,…,𝝆_n-1 are pseudo-randomly-sampled scalars. In terms of precompiled smart-contracts, it would take:
   (2n-4) x ECADD  +  (2n-4) x ECMULT + ECPAIR_k=2 = (2n-4) x 6,150 + 113,000 gas.
2. Gas cost of storing data. Each participant also stores the update on-chain as calldata (68 gas per byte) accounting to n*64*68 gas. (A note for those familiar with elliptic curve cryptography: storing compressed points would make decompression dominate the overall cost as per our measurements for n=256.)

This brings us to the following table estimating gas costs which should inform future optimizations: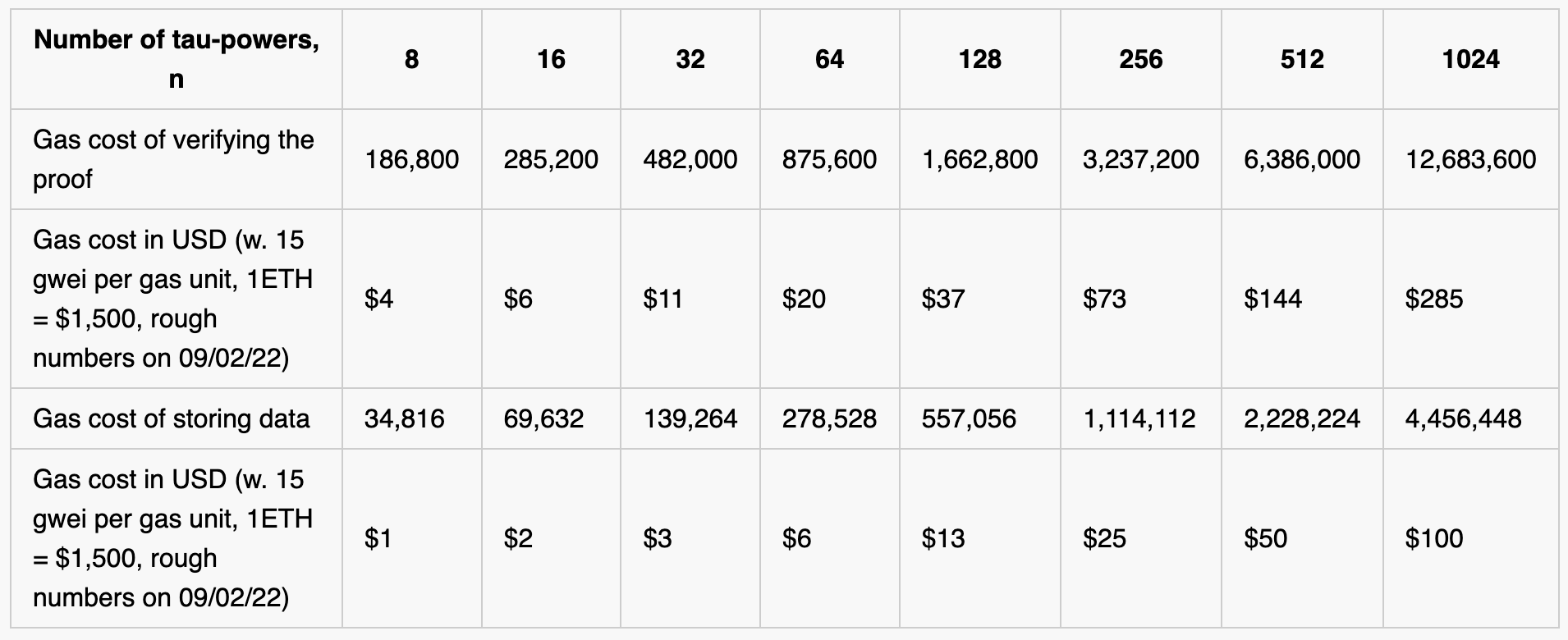We are exploring solutions to bring the gas-cost down, so stay tuned!

We’ve open sourced our EVM based powers-of-tau ceremony repo at github.com/a16z/evm-powers-of-tau. Conducting a ceremony with our strategy is easy and transparent:

1. Deploy the storage and verification contract (contracts/KZG.sol)
2. A contributor reads ceremony parameters from previous transaction calldata
3. The contributor generates a secret locally, computes the updated parameters
4. The contributor generates their proof: pi1, pi2
5. The contributor submits the updated parameters via KZG.potUpdate() to the deployed smart contract on the public blockchain
6. The smart contract will verify the validity of the update, reverting in the case of a malformed submission
7. Multiple contributors can execute steps 2-5 in perpetuity, each increasing the security of the ceremony
8. Whenever a developer is confident with the number and quality of submissions, they can query the blockchain for the current parameters and use these values as their cryptographic keys

Our repo uses arkworks-rs to compute steps two and three (the rust calculation can be found in src/pot_update.rs), but users may want to write their own. The entire end-to-end flow of update submission can be found in the integration test in tests/integration_test.rs.

Note that we have chosen to use calldata to store updated powers-of-tau parameters on-chain as it is several orders of magnitude cheaper than storage. An ethers-rs based query for this data can be found in src/query.rs.

Finally, proofs and detailed equations can be found in the technical report in techreport/main.pdf.

Before this trusted setup ceremony can be used in production, we’d recommend first having a comprehensive audit of both the mathematical proofs and the sample implementation.

As implemented the transaction cost of updating the ceremony grows linearly with the setup size. For most applications (SNARKs, DAS) we’d want a setup of n >= 256, currently costing $73 per update.

We might be able to achieve sublinear verification cost growth with a STARK proof of the valid update computation and a vector commitment to the updated values. This construction would also remove the dependency on the Ethereum L1 BN254 precompiles, enabling the usage of the more popular BLS12-381 curve.

All ceremony strategies have tradeoffs. We think this construction is solid and has great verifiable censorship resistance properties. But again, we would caution against using this method until more work is done to verify our approach’s soundness.

• Dan Boneh – for useful feedback at the early stages of this work
• Joe Bonneau – for clarifying the exposition in the early version of the technical report
• William Borgeaud – for discussion on BLS within TurboPlonk / Plonky2
• Mary Maller – for thoughts on the general mechanics of the approach

Editor: Robert Hackett @rhhackett

***

The views expressed here are those of the individual AH Capital Management, L.L.C. (“a16z”) personnel quoted and are not the views of a16z or its affiliates. Certain information contained in here has been obtained from third-party sources, including from portfolio companies of funds managed by a16z. While taken from sources believed to be reliable, a16z has not independently verified such information and makes no representations about the current or enduring accuracy of the information or its appropriateness for a given situation. In addition, this content may include third-party advertisements; a16z has not reviewed such advertisements and does not endorse any advertising content contained therein.

This content is provided for informational purposes only, and should not be relied upon as legal, business, investment, or tax advice. You should consult your own advisers as to those matters. References to any securities or digital assets are for illustrative purposes only, and do not constitute an investment recommendation or offer to provide investment advisory services. Furthermore, this content is not directed at nor intended for use by any investors or prospective investors, and may not under any circumstances be relied upon when making a decision to invest in any fund managed by a16z. (An offering to invest in an a16z fund will be made only by the private placement memorandum, subscription agreement, and other relevant documentation of any such fund and should be read in their entirety.) Any investments or portfolio companies mentioned, referred to, or described are not representative of all investments in vehicles managed by a16z, and there can be no assurance that the investments will be profitable or that other investments made in the future will have similar characteristics or results. A list of investments made by funds managed by Andreessen Horowitz (excluding investments for which the issuer has not provided permission for a16z to disclose publicly as well as unannounced investments in publicly traded digital assets) is available at https://a16z.com/investments/.

Charts and graphs provided within are for informational purposes solely and should not be relied upon when making any investment decision. Past performance is not indicative of future results. The content speaks only as of the date indicated. Any projections, estimates, forecasts, targets, prospects, and/or opinions expressed in these materials are subject to change without notice and may differ or be contrary to opinions expressed by others. Please see https://a16z.com/disclosures for additional important information.